| Synopsis: This page presents a general overview of the useof models in evolutionary biology. The differences between adaptationaland neutral models are briefly discussed. The bulk of the material dealswith an overview of two types of adaptationalist models -- optimality andgame theory-- and ends with a comparison between them. Later pages willpresent a more detailed explanation of game theory. |
Contents
Assumptions -- Adaptation vs.Neutral Models of Evolution
Adaptational Models: Following thesuccess of Darwin and Wallace's theory of natural selection, most modernbiologists believe that most of the aspects of the morphology, behaviorand physiology of an organism represent adaptations. That is, these aspects of the phenotypeexist in a population because in the recent past they allowed their possessorsto reproduce more successfully than individuals with alternative traits.
Neutralist Models: However, one mustkeep in mind that adaptation is often only an assumption. In the1930s Sewell Wright (seereference) developed the main theoretical underpinnings of an alternativemeans of accounting for evolution based on genetic drift. This processworks well in small populations especially when competing traits conferlittle relative survival advantage over each other (these traits are saidto be adaptively neutral).
Extending Wright's work, others have shown that the particular traitsfound in a population can be the result of historical accidents. For instance,Ernst Mayr (certainly an adaptationalist) pointed out the importanceof the genetic makeup of a small number of progenitors or founders(reference) ofa population. More recently, Stephen Jay Gould has writtenextensively about the role of history and accident ("contingency")in determining the present phenotypes of members of a population and theactual range of organisms that exist at a given time (see reference).
It is fair to say that much of the value of the work of Gould and othershas been to force biologists to acknowledge that all aspects of the phenotypeneed not represent specific adaptations. The phenotype is in part an accidentand not an ideal design. In many cases a number of competing versions ofa phenotype might all do equally well, especially given the nature of environmentalchange. Thus, it is necessary to provide evidence that a particular phenotypicfeature represents an adaptation, rather than provide circular "just-so"stories that purport to show adaptation by assuming it and then spinningout an explanation based on the (untested) assumption of adaptation.
Return to the frame's contents
Mathematical Models and RigorousScience
Mathematical models are abstractions that an investigator hopes willhave, to varying degrees of precision, predictive power. Models representthe scientist's best informed guess as to:
Mathematical models are useful because they take a scientist's ideasand produce a more complex abstraction (because a model consists of partsand their interaction). Complex, multi-element models often yield new insightsand novel predictions. Mathematical models have the advantage that theyyield quantitative predictions. Quantitative predictions are oftenless ambiguous than other types of predictions. Since tests of hypothesesare attempts to show the predictions are incorrect (tests attempt to falsifythe model), quantitative predictions are usually easier to test. Did themodel behave exactly as predicted or not? If not, how different was it fromprediction? How could the model be modified to make it more consistent withthe results and then re-tested?
Inability to falsify the model does not validate it. Inabilityto falsify means nothing more than that. Not showing that a model is wrongmeans only tentative acceptance, not proof of its truth. A modelthat has not been falsified is nothing more than a useful working hypothesis.For example, a telling observation was made by Dr. David Norman about restorationmounts of dinosaurs (these mounts are, of course, nothing more than hypotheses)when he wryly observed "we've got it right -- for now". Much ofthe formalism of testing and describing the scientific process can be tracedto the work of the English philosopher Sir Karl Popper (see reference) . (For a reference to Ernst Mayr's extendedand fascinating treatment of biological methodology press here).
Most commonly, models are modified as the result of (i) experimentalfalsification of one or more of their components or (ii) independent refinementsin our understanding of the variables and interactions that make up a model.You have probably noticed that this same process is normally followed throughoutthe scientific process; a main difference is that hypotheses in the formof mathematical models are often more concrete and quantitatively predictivethan are other types of hypotheses. However, keep in mind that working withexperimentally supported quantitative models is fraught with the same dangersas with less quantitative models -- like any hypothesis models should alwaysbe viewed with skepticism and only trusted to the extent that they havebeen strongly tested.
One other note about mathematical models in evolutionary biology: theycan spring from either an adaptationalist (reviewmaterial above) or a neutralist (review materialabove) view point. Two important types of mathematical adaptation-basedmodels are optimality and game theory models. The next twosections compare these two approaches. Since both are adaptation models,both will look for behavioral characteristics that maximize an individual'sreproductive success or some related variable.
Return to the frame's contents
Often a behaviorist is interested in predicting the best way (interms of its fitness consequences) for a particular animal to behaveirrespective of what other individuals are doing. To illustrate,suppose we are trying to understand how loudly an animal should make anadvertisement call (one designed to attract a mate). Thus, we are lookingat a general behavior (producing an advertisement call)and we are trying to understand the selective forces that determine thebest way to perform a particular part of the behavior -- in this caseits loudness. In this particular example (and in all optimalitymodels) we start from the assumption that the loudness of other callershas nothing to do with predicting the loudness of a given individual. Sowe might imagine a situation where an animal calls without others nearby(as would be the case in many species of crickets).
Optimality theory is adaptational - thus it springs from the theory ofnatural selection which predicts that an animalshould behave so as to maximize its fitness. All behaviors can be viewed as having bothfitness benefits and fitness costs. Since optimality modelsare quantitative, a first step will be to establish the relationships betweenthe variable of interest (the decision variable) and the associatedcosts and benefits. Benefits (B) and Costs (C) are kept strictly separate(just as is practiced in business bookkeeping) and thus two separate relationships(benefit vs. the decision variable and cost vs. the decision variable) areimplicitly part of the process of setting up an optimality model. Noticethat since we assume that the behavior (decision variable) has consequenceson fitness, the behavior is the independent variable for each of these relationshipswith benefit or cost being the dependent variables.
Now,since the fitness consequence of behavior is:
Net Change in Fitness = Benefit - Cost
the solution to an optimality model is to find the point where B-C is maximized.
In principle this formulation is easy to understand. However in practice,it can be more complex. Let's return to our example of call loudness toillustrate the process of constructing and solving a simple optimality model:
In acoustic communication, producing a loud call is energetically expensive(see reference). However,louder calls tend to attract more mates, (for example, see reference dealing with mole crickets).We want to construct an optimality model in order to try to predict howloudly to call with the "goal" of maximizing lifetime fitness.
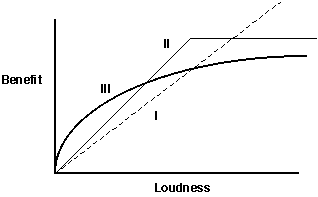
Let's start with the benefits of calling more loudly for a certainperiod of time. In theory there are a number of possible relationshipsbetween loudness and benefit. One would be linear -- get louder and proportionatelymore mates will come (graph I, below). A little reflectionwould suggest that this cannot go on forever -- at some point increasingloudness brings in so many mates that the focal animal can't handle allof them and so there is no further increase in fitness with loudness (graphII, below). Alternately, one might assume that the rate at whichmatings increase drop off before finally reaching a maximum (graph III,below) -- i.e.,because of other things the caller has to attendto, as the number of mating opportunities increase, the percentage thatare actually consummated becomes less:

There are several things to note about these plots:
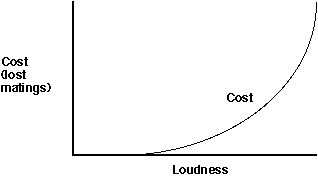
Costs Curves: It is logical to assume thatloud calling will have consequences on fitness since it costs considerableamounts of energy and therefore could weaken the caller. This leadsdirectly to expressing cost as energy loss (energy is something which I,as a behavioral physiologist, feel very comfortable with -- it can be measureddirectly and relatively easily). But absolute energy terms such ascalories or joules may not be the most relevant way to measure the energyportion of the cost of calling. For instance, if the cost of getting louderis viewed relative to energy stores, low cost calls might have littleimpact on reserves and therefore,up to a point, increasing loudness mighthave little accompanying increase in cost. However, when the energy demandsof making louder calls increases beyond a certain point, they may significantlyaffect an animal's energy reserves and therefore force it to either callfor a shorter time period (perhaps thereby lowering its fitness) or eatless (also lowering its fitness). Notice that once again, the exact positionand shape of the curve would depend on many factors -- for instance sizeof food reserves and the ease with which they are replaced relative to theincremental costs of louder calls.
Moreover, another important cost of calling is increased chance offalling victim to predation (e.g., see Mike Ryan's work on bats preying on calling frogs). Whatunits do you use to measure this cost? The cost could be expressed as thechance of being killed or injured, or better yet the number of future matingsor future offspring lost as a result of injury or death associated witha certain loudness of call.
Let's assume that we believe there are just two important costs to calling-- energy and risk. We need to combine these into one cost relationship.Both are already related to the same decision variable (loudness) but thesetwo types of costs are usually expressed in units that are different fromeach other (for example joules for energy and probability of death for predationrisk).
If we want to combine all costs into one curve,we need to put them into a common unit of measurement (a common
Now let's complete and solve our model. Let'ssay that we decide that benefits model III (review graph of benefits) is the best one to use. Ifwe now express benefits and costs of call loudness in a currency of numberof successful matings, then we can superimpose the benefit and costs ploton the same axis and then solve for the loudness that gives the greatestincrease in fitness as measured by the greatest number of matings:
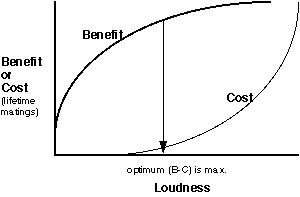
Notice that the model predicts that the best loudness to call is notthe loudest (which is what you would predict if only benefits had been considered).Notice also that in this case, the model does not keep costs to an absoluteminimum.
We can use the B and C curves (above) to make another graph, this timeof B- C vs. loudness, to illustrate the optimum another way:
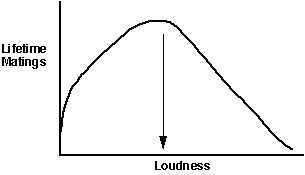
This type of depiction clearly shows that the greatest lifetime fitnessin our hypothetical situation is achieved by calling with some type of intermediateloudness.
Finally, realize that the model is nothing more than an integrated setof hypotheses that together attempt to predict the best loudness to call,irrespective of what others are doing. As we saw above (pressto review general info. on mathematical models), this prediction willneed to be tested (for instance by attempting to determine the lifetimemating curve for animals of different loudness). In practice, this essentialstep is often very difficult (think how hard it would be to determine thecurve given above for some type of animal) and much of the art and hardwork of behavioral science lies in these tests of the models.
Return to the frame's contents
A Brief Introduction to Game Theory
OK, we just went through a long introduction to an important topic inbehavior, physiology, and ecology: optimality theory. But you thought thiswebsite was about game theory. It is. The stuff on optimality (above) wasimportant because you need to know something about optimality theory tounderstand game theory and especially to understand which techniques touse when trying to understand animal behavior.
So, what is game theory? In optimality theory it is assumed thatwe can predict the best behavior for a particular (focal) animal irrespectiveof what others are doing. However, the frequency with which others are performinga particular behavior is often highly relevant to the fitness consequencesof acting a certain way. Thus, the crucial aspect of game theory is thatselection among alternative behaviors depends to a large degree onwhat others are doing. A behavior that works very well when rarein a population (for instance, some type of deception) may not be nearlyas advantageous to its actors when it becomescommon. Thus explorations of game theory involve studies of a form of
Here's a brief example. Let's return tocalling behavior. Let's assume that females are attracted to calling malesand travel to them to mate. But let's also assume that arriving femalesare not infallible in spotting the male that actually was making the callto which they were attracted. Or, females may be intercepted by males asthey approach and sometimes the intercepting males were not the ones thatattracted the female in the first place.
What's the best thing for a male to do? If no one is calling, it is probablybest to call and become conspicuous to females interested in mating. However,if there are many callers, it might be best to keep quiet (avoiding energyand predation risk costs -- reviewprevious material) and try to intercept females as they approach a callingmale. Such a male is termed a satellite.
As a strategy satellite could well be as or more fit than calling, dependingon its frequency relative to callers. Thus, even though a satellite mighthave fewer opportunities per day to mate (lower benefit), the fact thathis costs are less means that he might have as many if not more lifetimeopportunities for mating. However, as should be obvious, his relative successdoes not simply reduce to costs and benefits as in optimality theory --instead, his fitness depends very much on the frequency of callers (vs.satellites) in the population. If few others call, satellite is probablynot a good strategy and relatively speaking, calling is an excellent strategy(or taking it to an extreme, if no one is calling, the silent satellitestrategy makes no sense since females are attracted to calling males). Onthe other hand, as more and more callers are present, satellite works betterand at some frequencies might over a lifetime payoff better than calling.Thus, frequency dependence distinguishes this example from simple optimality.
| ! Note: don't get the idea that I am arguing here that satelliteis generally a more or less fit strategy than the alternative, call. Dependingon conditions, at any moment in time all of these are possible. Later wewill consider the most interesting outcome of evolutionary games, an evolutionarystable strategy (ESS). We will see that one type of ESS (mixed ESS) predictsthat both strategies would coexist at constant relative proportions to eachother and at these frequencies the fitness of individuals of each strategyare equal. |
Summary : Notice the similarities and differences between optimalityand game theory. Both deal with the benefits and costs of a behavior. Insituations where optimality theory is applicable, that is all that is needed.However, as in the example above, there are many cases where the fitnessassociated with a particular behavior depends on what others are doing --that is, fitness is frequency-dependent. Thus, what is best willdepend on what everyone else in the population is doing (and therefore onthe likelihood of certain types of interactions with certain types of fitnessconsequences).
You now have a basic idea about the uses of mathematical modeling instudies of behavioral evolution. You should also be familiar with the basicsof game and optimality models. You may now continue on to a more detailed introduction to game theoryespecially in regards to an important concept, the evolutionary stable strategy,or you may continue reading this page and learn a bit about the historyof game theory.
Return to the frame's contents
A Brief Sketch of the History ofGame Theory
Game theory is equally useful in studies of learned and innate behavior.In fact, when originally developed by von Neumann and Morgenstern (reference) during the mid 20thcentury, it's primary purpose was to understand the most rational way forhumans to make decisions between alternative courses of action, in particularas they applied to economics.
However, any technique that will allow us to study the payoffs of a learnedbehavior can be used equally well to study innate behavioral strategies.John Maynard Smith (1982) points out that the idea of rational interestin economics is simply replaced by the concept of fitness. He traces theuse of game theory in biology first to the work of Lewontin (see reference) (1961) and later Slobodkin and Rapoport(see reference).These workers applied game theory to situations of "species or groupsurvival" (Did you ever play the board game "Extinction"?).The present mainstream of game theory began with Hamilton (1967) (see reference) and then afew years later with Maynard Smith and Price (1972) (see reference) and then Maynard Smith (1974) (see reference). In the interveningyears, game theory has been adapted by a number of biologists to examineevolutionary problems-- hardly an issue of Animal Behaviour passeswhen one does not see an article using game theory.
Perhaps the most thorough introduction to the use of game theory in biologyis by one of the pioneers in applying it to biology -- John Maynard Smith(1982) (see reference). The interestedand mathematically inclined student is urged to read his classic introductionto the field. The material at this site is based largely on the the firstfew chapters of his book. However, most students will find that Riechert and Hammerstein's 1983 article in the AnnualReview of Ecology and Systematics is more readable and is highly informative.
Continue on toa Detailed Introduction to Game Theory
Return to the frame's contents
Copyright © 1999 by Kenneth N. Prestwich About FairUse of these materials Last modified 12 - 1- 09 |