Continuous variable: a variable with the property that between any two values, there are an infinite number of other values. Synonym -- analog variable.
Cumulative probability distribution (examples: Q(x) or P(x)): the cumulative chance of some event with respect to the independent variable. For example, if the independent variable is cost, then P(x) might indicate the total proportion of times (or individuals) who have quit as of a certain cost. Thus, this would vary between zero (no one has yet quit) and 1.0 (everyone has quit).
delta Q(x): for our purposes, the probability that a mix strategist such as var will pay a particular cost x and then quit. It can be computed by determining the probability of paying cost x (Q(x)) and cost x - dx (where dx is some small increment of x) using the cumulative probability function. The difference Q(x-dx) - Q(x) is delta Q(x) and is equal to the chance that an individual paid cost x and quit.
Discrete Variable: a variable that can only possess certain exact values -- intermediate values are not possible and are rounded to the nearest permitted value or in rare cases are simply ignored. Synonym: "digital" value.
e: the base of the system of natural logarithms, approximately equal to 2.7183.
Equilibrial Strategy: in our context, a strategy that is NOT increasing relative to any other as a result of selection. Thus, all equilibrial strategies within a population must have the same fitness. Equilibrial strategies may or may not be evolutionarily stable. Press here for more information.
exp(): the base of the natural logarithm system e raised to the power inside the parentheses. Note that when the value in the parentheses is negative (a negative exponent of e) that this is equivalent to 1/exp(). Thus, exp(-2) is the same as writing e^-2 or 1/e^2 or 1/(2.7183^2).
exponential decay distribution: a
distribution that results from applying a constant rate of continuing to
the members of some initial population. So, for each value of x, the chance
that an individual will chose to continue is constant.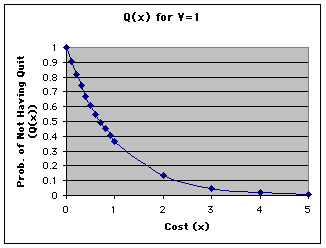 
Now,
since not all continue from one value of x to the next (those that don't
continue quit and are not longer in the population of players) the population
decreases with x. Since the population is decreasing but since each member
of it always has the same chance of continuing, the greatest number quit
at first, with fewer at each subsequent step. The result is a curve such
as the one at the left. You
can read about exponential decays in more detail by pressing here.
fix(x): a fixed cost (or fixed display time) strategist equivalent to the fixed cost strategies Maynard Smith (1982) termed a,b,c ... etc. In the notation we are using here x refers to the cost that fix is willing to pay (its value of m). Thus, x can have any value but when contests are written as fix(x) vs. fix(x) assume that x has the same value for each contestant (i.e., each has the same m).
m: some maximum cost that a contestant is willing to pay. Thus it is a specific value of x (cost) or t (time). On many occasions m is used simply to symbolize the maximum cost that some arbitrary focal individual in a given contest will accept. That is the definition we use on this page-- most commonly as a maximum cost that a pure strategy is willing to pay as compared to what a variable cost (mix) strategist might pay. It is used inconsistently in the literature -- often m is the cost paid at the termination of a contest. Thus, since contests terminate when the cost exceeds what one player is willing to pay by a tiny amount (dx), then this cost (which represents the maximum acceptable cost to the loser becomes m. Sorry for the confusion.
Pseudorandom Number: the result of a "random" number generation by a computer. The computer uses an algorithm to generate a numbers; numbers generated by this means fit models for randomly distributed numbers. However, since a defined set of mathematical operations produce these "random" numbers, they are not random in the truest sense of the term. Many mathematicians and computer scientists have pointed out that there are subtle differences between numbers generated by computer algorithms and those generated by, for instance, observing motion of molecules (or even mixing balls in a lottery machine!). However, for our purposes, pseudorandom numbers are just fine -- we will never notice the difference. The term is used simply to remind you that computer generated random numbers are not truly random!
p(x): the probability density function of cost (x). The function that can be used to find the probability of any supporting strategy in the mix; finding this function was Maynard Smith's main task in describing a mixed ESS to the symmetrical war of attrition. Important Note: this function gives the probability per unit cost and must not be confused with a function that gives probability per se. In the war of attrition, a probability density function is used as a central element of the description of a variable cost strategist.
P(x): the cumulative probability distribution function of cost (x). This gives the cumulative probability of some event (for example, quitting display) as a function of some independent variable (in this case, cost (x)). It is calculated as the integral of the probability density function. We use P(x) to indicate the cumulative proportion of a population who have quit as of some cost x.
Q(x): the cumulative proportion of individuals who have not quit (are continuing in the contest) as of some cost x.
rate constant: a constant in the exponent of an equation of exponential decay that determines the how fast the dependent variable (for example, chance of quitting) changes with respect to the independent variable (for example cost). For the var strategist, the rate constant is 1/V so the larger the value of the contested resource (V), the smaller the rate constant and therefore the less the independent variable (e.g., probability of quitting) changes per unit time. Thus, for cumulative probability distribution P(x) = 1 - exp(- rate constant*x) and since in this case the rate constant=1/V then P(x) = 1 - exp(- x/V).
Supporting Strategy: any pure strategy (unique cost in the war of attrition) that is a member of the mixed ESS. Alternatively, it is any unique cost (in the war of attrition) that a mixed strategist plays. A good synonym is component (of the mix) strategy. For example, in the Hawks and Doves game, if injury cost is greater than V, a mix with supporting (component) strategies "hawk" and "dove" results.
t (time): a cost measured in terms of time spent displaying. When the symbol t is used, it is meant to refer to a universe of possible values of display times. A given t (e.g., t1) refers to a specific time. A useful metric since display time is easy to measure and understand and since fitness costs (x) are usually a simple function of time.
x (cost): any display cost in some sort of units that can be converted to fitness. Normally used interchangeably with time of display (t) since x = f(t) where f(t) can be any function that converts time to cost. At this website we always assume that cost is a linear function of time (t = m*t +b where m is the slope and b the y-intercept) but there is no reason to assume that this will always be so.
V: the value of the contested resource; its reciprocal equals the rate constant in the probability density function and cumulative probability distributions for var.
var: a variable cost (variable display time) strategist equivalent to the mixed strategy Maynard Smith (1982) termed I. It is composed of all possible costs (equivalent of all possible fixed cost strategies) each played with frequency determined ultimately by a probability density function.