Evolutionary Competition of Alleles or Organisms -- The Concept of Fitness and its Measures
While the unit of evolution is the population, nevertheless, selection occurs between individuals bearing alternative phenotypes (which for our purposes will mean individuals using different genetically based behavioral strategies). Since different phenotypes spring partially from alternative alleles, selection can also be seen as a competition between alternative alleles. There are a number of ways to measure the success of different individuals or alleles. All involve the fitness concept.
The term fitness comes from Darwin and Wallace's idea that animals that survived (i.e., were most fit) were most likely to leave a greater number of offspring. While the notion of survival primarily has to do with what they termed "natural selection", we will also to include the effects of sexual selection on an individual's reproduction when we discuss fitness.
| Note: for the purposes of our present discussion, we will leave out concepts of indirect and inclusive fitness. |
Simply put, fitness is a measure of the number of copies of an individual's genes, or if we are considering a single genetic locus, the number of copies of an allele, that are put into the next generation.
! Actually to get around some of the problems that can arise when an individual's offspring (F1 generation) are infertile (F2 generation), the most formal analyses count the number of grandchildren (F2). There are well-known examples of this sort of thing, termed hybrid sterility -- think of donkey and horse cross. It yields a vigorous, valuable F1 (mule) but no F2 -- mules are sterile. Nevertheless, in cases where there is no reason to suspect hybrid sterility, it is common practice simply to count the numbers of offspring. |
Fitness is abbreviated by with a W with some other notation that usually explains whose fitness is being considered (e.g., W(Hawk) for the fitness of the strategy Hawk). Simply counting the number of offspring or grandchildren gives a measure that can be called absolute fitness.
Relative Fitness: Evolution is a numbers game and so what really matters in generational competition is not the number of offspring (provided it is more than 0) but how many an individual produces relative to its competitors. The simplest way to make this comparison is to just compare how many copies of each allele are produced -- for example, strategy A (associated with allele A) produces and average of 1.7 offspring while strategy B produces 2.2. One can easily see that strategy B is doing better. But how much better?
Humans have a very good understanding of proportional measurements -- where 1.7 vs. 2.2 tells us something, saying that strategy A is only 77% as successful as strategy B usually tells us something that we understand better when we are considering the outcome of competition. Using measures of relative fitness do just this sort of thing. They arbitrarily define the most successful type as having the reference fitness. All others are measured as a proportion of this reference value. Thus:
| Fitness = W = | average # of offspring by any strategy |
| ---------------------------------------------------- | |
| average # of offspring of most fit strategy |
and for the example we just considered:
Assume that a population of asexually reproducing organisms possess two genetically determined behavioral strategies, A and B. Assume that, taken as groups, A and B strategist's fitnesses differ only as a result of how their behavior affects their ability to reproduce (in other words, they differ only in regards of being A or B strategists). These animals live one year and the average number of offspring left by an A strategist is 0.85 and for a B strategist it is 1.05. At the start, there are 850 individuals of strategy A and 125 of strategy B. (a) What is the frequency of strategy A? strategy B? ANS (b) What are the relative fitnesses of strategy A and B? ANS (c) What will be the frequencies of the two strategies in the next generation? ANS (d) At present, is the population size as a whole increasing, declining, or steady? ANS (e) If evolution continues and if the relative fitnesses of the two strategies remain the same, predict what will happen to the population as a whole -- will it increase, decrease or remain the same? ANS |
Copyright © 1998 by Kenneth N. Prestwich
About Fair Use of these materials Last modified 8 - 29 - 98 |
(a) What is the frequency of strategy A? strategy B?
ANS: There are 850 individuals of strategy A and 125 of strategy B at the start for a total population size of 850 + 125 = 975
As with any calculation of frequency:
# of members of the group / total population size
so freq.strategy A: 850 / 975 = 0.872
and since there are only two strategies, then:
freq strat B = 1.0 - freq strat A = 1.0 - 0.872 = 0.128
checking using the formula above: 125 / 975 = 0.128
(b) What are the relative fitnesses of strategy A and B?
ANS: Strategy B leaves an average of 1.05 offspring vs. only 0.85 for strategy A. Thus, using the formula for relative fitness:
(c) What will be the frequencies of the two strategies in the next generation?
ANS: Since we know the average number of offspring produced asexually by members of each strategy, we simply multiply that number times the number of individuals to get the number in the next generation:
for strategy A: absolute W(A) * # A parents = 0.85 * 850 = 722
for strategy B: absolute W(B) * # B parents = 1.05* 125 = 131
total offspring (size of F1 generation) = 722 + 131 = 853
new freq(A) = 722 / 853 = 0.846
new freq(B) = 1.0 - 0.846 = 0.154 -- B is increasing and A decreasing (surprise! -- after all A is less fit).
Notice you can also do this by multiplying the frequencies or the numbers of individuals times the relative fitnesses and finding the frequencies:
first for numbers times relative fitness:
strat A = 850 * 0.81 = 688
strat B = 125* 1.0 = 125
total = 688 + 125= 813 (note that this is not the actual size of the new population since we used relative fitness, not the absolute fitness (the average number of offspring).
freq strat A = 688 / 813 = 0.846
freq strat B = 125 / 813 = 0.154
Or, using freq. and relative fitness:
for strat = rel. fitness * freq.
Strat A = 0.81 * 0.872 = 0.706
Strat B = 1.0 * 0.128 = 0.128
total = 0.706 + 0.128 = 0.834
Note that all of the calculations above are in proportions, not numbers of individuals
freq Strat A = 0.706 / 0.834 = 0.846
freq Strat A = 0.128 / 0.834 = 0.154
(d) At present, is the population size as a whole increasing, declining, or steady? ANS: the population is declining -- from 975 to 853. While the population is declining, at the same time it is evolving more towards strategy B!
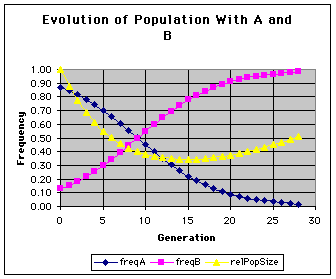
(e) If evolution continues and if the relative fitnesses of the two strategies remain the same, predict what will happen to the population as a whole -- will it increase, decrease or remain the same? ANS: the population will continue to decline until most A strategists are gone (since they only leave 0.85 offspring), When the frequency of strategy B (which leaves 1.05 offspring) reaches a certain point the population will begin increasing again. In our example, this happens at about generation #15 (note in this graph, the total population size is expressed relatively to the first generation):

Note that this particular pattern is not required for evolution to work -- it is possible that a population could be increasing the entire time one strategy was out-competing another!