| Synopsis: The material on this page is not directly connected with most of the game theory website. It contains an illustration of the importance that frequency can have in determining fitness. The example is from communication theory (see Harper 1991) and deals with situations when an animal would be expected to evolve resistance to dishonest signals. It illustrates how the fitness consequences of a particular type of interaction depend not just on its costs and benefits but also on how often it occurs. |
Both game and optimality theory look at the consequences of actions in terms of their net profitability as defined by the costs and benefits of a particular behavior; ultimately these impinge on fitness, W. Game theory also factors in the influence of the behavior of other individuals. In game theory the fitness associated with a particular behavioral strategy is determined by the net benefit or cost (payoff) of each type of interaction times the frequency with which these interactions occur. Thus, to understand game theory, one must begin with an understanding of how the frequency of different encounters might effect fitness.
The example of frequency dependent selection on this page IS NOT AN EXAMPLE OF GAME THEORY. It deals with the selective forces acting on a receiver of "honest" (cooperative) and "dishonest" communications. It is taken from Harper's 1991 treatment and has been modified somewhat. While this example is not a game, we will use it gain insight into frequency dependence and to introduce us to some of the conventions and techniques used in game theory.
| ! A Warning: you should think of this model is a reasonable hypothesis that is in need of testing -- as with all of the models explained on this website, don't be seduced by the logic of the argument into believing the model is true as written without testing. |
Return to the contents at the top of this frame.
Let us analyze one way that selection will act on receivers of a signal. Suppose that a cooperative ("honest") system of communication exists. The receiver gains a benefit B each time it responds to the honest signal. Assume that there is also a certain frequency of dishonest signalers; when the receiver responds to a dishonest signal it pays a cost C. Now:
| ! Note that B is not required to equal C -- in fact in most cases they will not be equal. |
What is the overall fitness of the receiver?
Let's represent these chances symbolically:
| eq. 1 | t = frequency of truthful signals |
and therefore t is the chance of receiving the benefit B. Likewise,
| eq. 2 | d = frequency of dishonest signals |
and therefore d the chance of paying costs C.
Since
there are only two types of signals, then according to what we know about
the calculation of frequencies (press here to review frequencies):
| eq. 3 | t + d = 1.0 |
and:
| eq. 4 | d = 1.0 - t |
We can now write equations for the lifetime fitness effects on an individual who cannot tell honest from dishonest signals and therefore responds to all. The lifetime benefit for heeding truthful signals is:
| eq. 5a | Lifetime Benefit = B * t |
Alternately, we could calculate this benefit using an equivalent of t (see eq. 4):
| eq. 5b | Lifetime Benefit = B * (1 - d) |
| ! The reason for expressing the same idea two different ways will be evident in a moment, so just hang on. |
By similar logic the overall fitness cost from dishonest signals is:
| eq. 6a | Lifetime Cost = C * (1 - t) |
or expressed equivalently in terms of the frequency of dishonest signals:
| eq. 6b | Lifetime Cost = C * d |
Now the overall effect of the signal and its dishonest counterpart on the fitness of the receiver is the sum of one of the lifetime benefit of heeding the honest signals plus the lifetime cost of falling for dishonest ones:
| eq. 7a | W(receiver) = Expected Lifetime Gain + Loss |
If we substitute eq. 5a for benefit and 6a for cost, into 7a we get:
| eq. 7b | W(receiver) = B * t + C * (1 - t) |
or, expressed equivalently using the frequency of dishonest signals (eqs. 5b and 6 b):
| eq. 7c | W(receiver) = B * (1 - d) + C * d |
When Should the Signal Be Ignored?
Both of these equations above stress that fitness of the receiver depends not only on the benefit to responding to honest signals nor only the cost of responding to dishonest signals, but also the frequency of each.
One way to view this graphically is first to manipulate the equation by:
The results are:
eq. 8a |
t = C / (C - B) (from eq. 7b) |
| eq. 8b | d = B / (B - C) (from eq. 7c) |
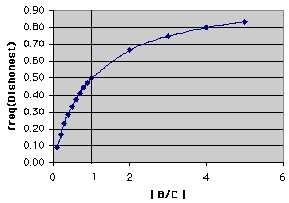
Now. let's make a graph of one of the equations and see what it might tell us. Here's the graph of eq. 8b

| ! Note: In this graph, we expressed B and C as the absolute
value of the ratio B/C. The reason for using absolute value was that
we added costs and benefits and therefore costs always had to have a negative
sign. The reason for using the ratio is that we have two variables (B and
C). Using a ratio is the equivalent of setting one of the variables (e.g.,
C )to some value (e.g., C = 1) and then solving for a series of values of
B. So, any B/C ratio less than 1.0 means that the absolute value of the cost of heeding a dishonest signal is greater than the benefit of heeding an honest signal; conversely ratios that are greater than 1.0 imply that benefits to heeding honest signals are greater than the costs of falling for a dishonest mimic. |
Now, what does the graph tell us? The plot itself can be termed an isopleth or isofitness curve. Every point on it shows the maximum frequency of dishonest signals that an individual can tolerate for a certain ratio of benefits and costs if the net effect on lifetime fitness of the receiver is to be zero (remember that this receiver cannot tell honest from dishonest signals). Other isopleths can be drawn for other lifetime fitness effects -- positive and negative. The graph below shows the same plot with additional isopleths for W = - 0.5 and W = 0.5:
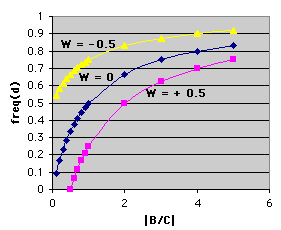
These extra isopleths make a useful point. Notice that for a given ratio of B/C, the fitness effects of increased frequencies of deceitful signals lower the fitness of the receiver. Note also that all of the isofitness curves show that as B/C increases, the frequency of dishonest signals that is tolerable for a certain lifetime fitness in the receiver increases. Both of these are intuitively satisfying results.
So. let's go back to the line where W = 0. This plot represents a mathematical boundary. Pick a value of B/C (for example, the vertical line drawn at B/C = 1). Any point on the W = 0 line that is above the plot represents a frequency of dishonest signals that will result in a negative lifetime effect on the fitness of a receiver that cannot tell dishonest from honest signals. Likewise, any point below the plot (the boundary) represents a frequency of dishonest signals that is not so high that it completely negates the benefits of the honest signals (that first happens at the line).
! A quick example -- assume that B = 1 and C = -1 for an animal that heeds the signal. In other words, the absolute magnitude of the benefit of honest communication and cost of falling for a dishonest communication are the same (but one is a cost and one a benefit). According to eq. #8b the critical value for the frequency (proportion) of dishonest signals is 0.5. Let's assume that in reality 0.6 of the signals are dishonest. For a receiver that heeds the signal, B *(1-f) + C*f = 1 * (1 - 0.6) + (-1) * 0.6 = - 0.2. This is less than the value for individuals that might totally ignore the honest signal and its mimic. Therefore if this level of dishonest signals persists, there will be selection against individuals that heed the signal. (This will be true for any frequency of dishonesty for a given B/C that is above the W = 0 line on the plot) ! Another note -- remember that zero simply means that there is no consequence on the reproduction of the individual in terms of a cost (decrease) or benefit (increase). Implicit in this argument is that 0 in fact represents some base-line of reproduction that can be improved on with the addition of benefits or decreased with costs. |
|
What about effects where Costs or Benefits are extremely high and do not simply represent slight modifications of fitness? Look at the following example and think about costs and benefits. Following are a series of simplistic questions that assume that these insects are far less behaviorally sophisticated than they actually are -- but nevertheless, use the questions to clarify your ideas about relative costs and benefits. Let's consider Jim Lloyd's (homepage or reference) famous example of firefly femme fatales. Firefly males normally fly about and advertise their interest in mating while females remain perched. Conspecific females answer with a species-specific flash pattern of their own (a certain color, duration, and pattern of flash). The communication between conspecific female and male is mutually beneficial and constitutes an honest communication. In this case the male is the receiver and he gains a benefit B (mating -- what could be more basic?) for responding. Lloyd showed the females of certain different species (the femme fatales of our example) are able to mimic the flashes of the females of other species. They produce these dishonest signals in response to the male's advertisement flashes; when a male approaches one of the femme fatales too closely he is seized and eaten, injured, or if lucky he escapes having only lost some time. Therefore males that respond to the dishonest signal pay a cost C. Let's make the simple-minded assumption that males cannot tell the honest from dishonest signals (again, this may not be strictly true since males in areas where femme fatales occur are very wary and approach carefully -- perhaps because something isn't right, perhaps because wary males have been selected for in these areas). Now, to recapitulate, the male is the receiver who gains B from responding to a conspecific female and pays cost C when responding to the dishonest signal of a femme fatale. Questions: (ii) Suppose that males always die when they respond to a femme fatale and suppose that the only way they can mate is in response to a female's signal. Should males tolerate a high frequency of dishonest signals? (Discussion) (iii) Does tolerating a high frequency of dishonest signals mean that selection pressure to find ways to avoid being snared by a femme fatale is low? (Discussion) |
Notes and References
Harper, D.G.C. 1991. Ch. 12: Communication (especially p 388). In: Behavioural Ecology: An Evolutionary Approach. J.R. Krebs and N. B. Davies eds. Blackwell Scientific Publications.
Lloyd, J. (1965) Aggressive mimicry in Photuris firefly femme fatales. Science 149: 653-654.
Endnotes and Answers to Questions
About Costs: Assume that COSTS have a negative or negligiable effect on fitness (C < = 0) while BENEFITS always have a positive or negligable effect on fitness (B > = 0). This assumes that an individual is capable of reproduction independently of the behavior under consideration and that benefits increase this reproduction over some baseline (usually defined as zero) whilst costs decrease the reproduction from baseline. This is a convention that is consistent with the equations written in this section; costs can be expressed in absolute terms if appropriate changes are made in the equations. Return to where you were in the text.
About Resistance to Dishonest Signals: Once a dishonest signal evolves, clearly there will be selection pressure to be able to tell honest from dishonest. The greater the costs to falling for the dishonest signal, the greater this pressure. As resistance to the dishonest signal evolves there will be pressure to make the dishonest signal even more believable -- more like the one it mimics. We now have a classic co-evolutionary "arms race. In the example we are studying, we will avoid this issue and simply assume that the mimic is so good that the receiver cannot tell it from an honest signal and so the question becomes one of when to totally ignore the signal. Return to where you were in the text.
In this extreme case, it would seem that costs are lower in an absolute sense than are benefits. Why? Because, a beetle that does not respond to signals at all has zero fitness as does one that gets eaten. Since the males cannot tell the real from fake signals, they must play along to have any hope of reproduction -- not playing is not an option and therefore in this light, overall the cost of getting eaten by a femme fatale is not so great if the only other option is not playing the game! One could make the argument in this case that the cost is zero if you assume the baseline condition (of not using signals) is zero.
(b) If males can find other ways to mate in addition to using the signal system, have the relative values of B and C changed from the previous case? If so, how?
Now this changes things a bit. Essentially we have described a scenario where males can obtain some fitness without responding to signals. Responding to an honest signal gains an additional benefit B. However, responding to a dishonest signal causes one to lose the matings that might be achieved without signaling. Thus, costs become larger than in the previous example.
This is example (a) from the last question. Clearly males must be prepared to accept a very high level of dishonest signals since they have no other means to mating; eq. 8b predicts this. This situation is a good analogy to desperation!
(iii) Does tolerating a high frequency of dishonest signals mean that selection pressure to find ways to avoid being snared by a femme fatale is low?
Absolutely not! One expects to see selective pressure favoring ways to discern femme fatales from conspecific females to appear with the first femme fatale! The strength of this pressure will increase as the frequency of femme fatale increases. Besides leading to the ability to discern honest from dishonest signals, this pressure would also favor behaviors that are not directly concerned with the signaling system but that lower the chance of being eaten -- for instance the careful approach used by males in regions where femme fatales occur.
Copyright © 1998 by Kenneth N. Prestwich
About Fair Use of these materials Last modified 8 - 24- 98 |