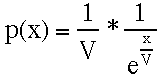
| Synopsis: This page shows the differences between the probability density function p(x) such as the one used to describe the mixed ESS var and the probability distribution functions such as P(x) and Q(x). A central idea is that p(x) has units of probability per x; calculation of probability therefore requires integration of p(x) over some range of x (i.e., taking the area under the p(x) curve between two values of x). As a result, there is a small amount of calculus on this page but all of it is thoroughly explained. Students who have not had calculus should read the sections and learn a bit about calculus. There is also discussion of discrete and continuous variables. |
Contents:
Probability Density Using Uniform Distributions as an Example
Using Probability Density Equations to Calculate the Cumulative Probability Function
We have seen that the mixed cost strategy we are calling var quits contests of different costs according to the following probability density function:
eq. #1: 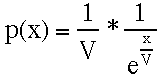 |
where p(x) is the probability density associated with paying cost x and V is the value of the resource.
Negative exponential distributions are an example of a very important group of functions called Poisson distributions. |
This equation is obviously very important. Unfortunately, it often results in some confusion. The main source of this confusion is that EQ. 1 DOES NOT CALCULATE THE PROBABILITY OF PAYING A PARTICULAR COST X. Solving eq. 1 for a few values of V will immediately illustrate why. Here are graphical solutions for V = 0.5, 1.0 and 2.0:
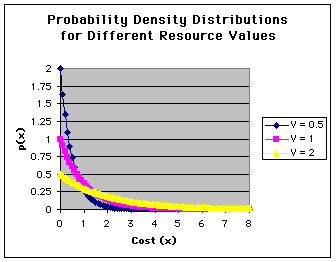
Notice that for cost = 0, p(x) can have values different from 1.0 -- for example when V = 0.5, p(x=0) = 2 (solution: p(0)= (1/V)*exp(-0/V)=1/V*1.0=1/V). Why does this matter? Recall that we are dealing with a game where individuals begin a display and quit at some cost x. In such a game, there should be a 100% chance that a contestant is present at the instant the game starts (if a contestant is not present, then it is hardly in the game is it?). Probabilities of 2 (twice certainty!) don't have a lot of meaning. Likewise, notice that if V = 2, then p(x=0)=0.5. Again, for there to be a game, the contestant must be there at the start!
| Note: you may recall from our earlier discussion that we showed that a fixed strategy that accepts a large cost relative to a resource is not evolutionarily stable against a fix(x=0) strategist. What is meant by fix(x=0)? Such an individual shows up for the start of the contest but then quits before the first tiny increment in cost, dx, is paid -- i.e., before the displaying gets started. |
(back to the contents and top of the frame)
Continuous Variables and Probabilities
So, what good is p(x)? The answer is simple -- probabilities can be calculated from p(x) using a technique we will see in a moment. Before we see how to use p(x) to get probability, let's take a moment to understand probability density functions a bit better. Why, you may ask, do we need this apparently round-about way of calculating probability?
The answer has to do with the nature of continuous variables (press here to review the differences between continuous and discrete variables). Let's say that we have theoretical reasons for believing that the cost paid by the contestants in a war of attrition varies continuously with time. If you some reasons, here's two:
Cost Can Be Either a Continuous or Discrete Variable We have just seen biologically meaningful examples where cost is a continuous variable. However, there are situations where only certain costs are possible. A starting example from human commerce would be the way most of us use money -- costs of goods are generally enumerated to the nearest small unit of currency -- for example, a cent, centimo, kopek, penny, whatever. Costs are rounded to these units, they generally cannot have any possible value. This is an example of discrete enumeration. Similarly, probabilities associated with discrete variables are often discrete. For example, "Head" or"tails" in a coin tosses are discrete variables. Exact probabilities can be assigned to each outcome and to each unique sequence of outcomes. Other intermediate values are not allowed. So, for example, an ideal fair coin has a 0.5 chance of either a "heads" or "tails" and so chance of flipping a fair coin four (independent) times and getting heads each time has a probability of exactly exactly 0.5^4=0.0625. Biological examples of cost as a discrete (or perhaps pseudo discrete) variable might include costs required to build a some object that is only functional if constructed a certain way and to completion. The same might be said of certain displays -- incomplete or variant or shortened displays might well be meaningless in the context they are presented. Thus, the constructed object or completed display becomes the discrete item of currency for the animal in these cases. |
To keep things simple, let's stipulate that cost, in theory at least, is a continuous variable and can therefore have any possible value. What is the probability associated with a particular value of a continuous variable? This may shock you -- as long as the continuous variable has a range greater than zero then the chance of paying any exact cost is very, very close to zero, regardless of the size of the range! Let's see why.
(return to the contents for this page)
An Example. A Uniform Distribution of Costs and the Probability of Each Cost
Let's assume that cost varies between 0 to 10 cost units (note: continuous variables can have upper and lower limits -- assume that animals never pay more than ten units because it kills them!). Let's assume that all values of cost between 0 and 10 are equally likely. Now, the sum of all of the probability of all of these values must equal 1.0.
Why? -- the costs between 0 and 10 constitute all instances. Remember that the sum of all instances in probability is certainty (a probability of 1.0.) Put another way, the chance of an individual event is the number of times it occurs over the total number of occurrences -- what we call probability is nothing more than another name for a proportion of the total instances of the variable. |
With this background, what is the chance of the value "exactly 5" if we are dealing with a continuous variable between 0 and 10 with all values having equal probability? It approaches zero and for all intents and purposes is zero. Why? Remember from number theory in your math courses that there are an infinite number of values between 0 and 10 for a continuous variable and for that matter there are an infinite number of values between 5.000000 and 5.000001. Thus since the total probability of all of these equally likely numbers must add to 1.0, then the probability of any one value is 1.0 / infinity -- essentially zero.
Let's see if we can find a way to depict this graphically. A useful (but not exactly equivalent analogy) is to imagine probabilities as particles or "atoms". Let's say that all particle possess exactly the same value (weight) of the total and that the weight of all of these atoms must always add to 1.0. (we are just being consistent with what we know about probabilities). And in this example they must be evenly distributed between 0 and 10.
The top graph below shows 10 such evenly distributed "atoms" each with a weight of probability of 0.1. But there could just as easily have been 1,000 or 1,000,000 or more atoms each with respective probabilities of 0.001, 0.000001 or less (it just hard to draw that many). You should be able to imagine such a graph with countless evenly distributed particles each with a very low value of probability or by analogy a low weight of probability:
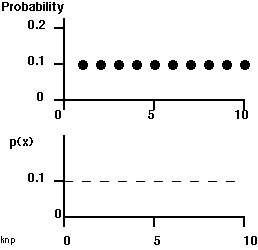 |
Now, let's divide the probability weight associated with each point (each "atom") by the small range of costs between it and the next cost. So, in the second graph in the frame above, since we have 10 evenly spaced 0.1 weight atoms, then each atom is separated from the next by 1.0 units of cost. If we divide the probability weight by the size of the increment (thus, 0.1 probability atom in each increment and each increment is x=1) and we get 0.1 probability units per unit cost.
Notice that if we do this same operation using a greater number of "atoms" (each with a smaller weight of probability and smaller range between it and the next atom) we always get the result of 0.1 probability per unit cost. This is because as we add more atoms, the weight of each diminishes and so does the distance to the next atom. So, if we produce an infinitely large number of atoms that are very short cost distances from each other (a distance that we will call "dx" (- see note)) we still get the same value.
You should now be able see what is meant by probability "density". We have just calculated probability per unit of the independent variable, cost (x). Imagine that instead of a graph we had a wire. The wire is composed of atoms, each with a certain mass. The more mass is packed into a given length, the more dense the wire. (if you're a physics buff this is a bit of imperfect analogy since density is usually mass per volume not length, but the analogy is nevertheless useful). So, our wire is made of probability atoms, each with identical masses. In this case, each atom is exactly the same distance (measured as a small increment in cost, "dx") apart and so the density of probability as function of cost is everywhere the same! Thus a graph of p(x) vs. x when each value of the variable has the same probability is a straight line with a slope of zero (see graph).
(return to the contents at the top of the frame)
Probability Densities in Non-Uniform Distributions
Constant probability density over the entire range of the independent variable is the exception, not the rule. So let's look at a more realistic example to be sure that we understand the idea of probability density. This time suppose that most of those atoms of identical probability are concentrated on one end of our 0 to 10 cost scale. So, the "atoms" are closer together (denser). If we divide their weights by the distance between them, we get a larger value when x is near 0 as compared to larger values of x. In the following graph, imagine that all of the individual probability atoms have the same density; greater over-all densities are shown by piling up the atoms:
 |
If it helps, imagine the higher value of the probability density p(x) as being the equivalent of more mass pushing down on a given unit of cost.
Thus, looking at a curve of a probability density function will give us an idea of where (in terms of the independent variable) events are more likely. BUT IT DOES NOT TELL US THE ACTUAL PROBABILITY OF AN EVENT. Recall that:
(return to the contents at the top of the frame)
Using Probability Density Equations to Calculate the Cumulative Probability Function
Unlike probabilities corresponding to exact values of continuous variable, probabilities over a range of the independent variable can be large enough to have some meaning. For instance, recall our first case of a uniformly distributed continuous variable that ranges from 0 to 10 that everywhere has a probability density of p(x)=0.1. The chance of any particular value is nearly zero but the chance of an event between 0 and 10 is is the sum of all of these near zero events, i.e., 100% (1.0).
Likewise, the probabilities of events falling between less inclusive limits can also be calculated algebraically. For instance, the probability that an event occurs between any x1 and x2 is the sum of all probabilities between x1 and x2. This could be calculated, for instance, as sum of all probabilities between 0 and x2 (which equals p(x)*x2 or 0.1*x2 in this case) minus the sum of all probabilities between 0 and x1 (=0.1*x1) -- that is: 0.1*(x2 - x1).
| Example: earlier we defined a situation where all values of x had a constant probability density of 0.1/ cost and where cost varied between 0 and 10. Thus, the probability of an event occurring between x=1.5 and 2.5 is 1.0*0.1=0.1; between 2.1 and 4.9 = 2.8*0.1=0.28. |
What we have just described is the equivalent of taking the definite integral of a function. In this case we take the integral of the probability density function.
Now, since in our first example p(x) equals a constant value; i.e., p(x)=k=0.1 then using the terminology of calculus we could symbolize an operation that determines the probability of paying a cost between x1 and x2 as:
eq. #2: |
where P(x1<=X<=x2) is the probability an event occurring between the two cost limits of x1 and x2 and p(x) is the probability density which equals the constant k in this example. All this equation says is that we find the difference in probabilities of all events between x=0 and x1 and x=0 and x2. The notation using the funny "S" sign (known as an integration sign) followed by kdx simply means to sum the product of k (here the probability per unit cost) times a series of very small differences in cost within the range of cost x1 to cost x2. This gives an answer that is a probability (since probability per cost times cost = probability).
About Calculus If you are uncomfortable with the calculus, go back and see that all we did was use different terminology to express exactly the same sort of idea that you might write down using algebra (review). You can easily re-write the previous equation as the solution on the right (i.e., k*(x2-x1)). There is no reason to be afraid of calculus; if you haven't taken calculus your goal should simply be to be able understand the equations -- you will not need to solve them. |
The last example was a trivial use of calculus. Furthermore, it was not useful to our gaining more insight into the mixed strategy var since var does not have a uniform probability density (i.e, with 'var', p(x) does not equal k). Instead, as we have seen earlier, the density of probabilities of quitting for var is an exponential decay (more like our second example of probability density). Trying to get an exact solution to the area under a curved line by using algebra (a discrete calculation) is computationally intense (we will use this type of method in conjunction with a computer spreadsheet, take a look at it to see how complex it can be!). Furthermore, such solutions are inexact. By contrast, calculus was invented to give us exact, easy solutions to such problems.
So, here we go. Let's use calculus to find the chance that that a var strategist quits between the start of a game where x=m = 0 and some later cost x=m>0. Once again, we integrate the probability density function:
|
|
where P(m) is called the probability distribution function -- the chance that an event occurs between cost = 0 and any cost x. P(m) is also called the cumulative probability function. Regardless, a plot of P(x) vs. x will give the chance that an individual plays to a particular cost and then quits.
Before we go any further let's look at eq. #3. Notice that all we did was substitute in the appropriate density function for the mixed strategy we call var (1/V*exp(-x/V)) instead of the constant k we used in our last example (eq. 2). We then integrated this between the limits of 0 and x. This is the equivalent of taking the area under the curve described by this function between cost =0 and=x (we need not worry about the mechanics of the integration that gives us the expression 1-exp(-x/v) -- if you have had calculus you probably remember how to do this and if not there is no need to worry about the mechanics).
Let's look at eq#3 and see if it makes sense. P(m) is supposed to be the chance of having quit by some cost x. Thus, it includes quitting at any time between the start and cost x=m. Notice that if cost x=0, then exp(-x/V)=exp(-0/V) = 1 and P(x) =1-1=0. This is what we would expect -- no one should have quit before the game has really started. Likewise, if the contest is infinitely long, then 1 - exp-infinity/V) = 1-0 =1 -- we expect everyone to quit by the "time" we get to infinity!
To review, we have seen that it is a simple matter to go from the the probability density function of var, p(x) to an equation that gives us the probability of having quit by a certain cost x=m, P(m):
eq. #4: 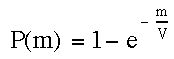 |
One final equation. What if we are interested in knowing the probability that an individual will quit somewhere between two different costs, x1 and x2? The solution to this is like what we saw earlier for our simple constant probability density model. This time we simply integrate var's probability density function between two costs x1 and x2:
eq. #5: Calculation of the probability that var quits between costs m1 and m2 (here termed delta P(m)):
|
Congratulations. You have the basics down of probability densities. Try the problems below to be sure that you understand this page:
(return to the contents at the top of the frame)
|
1. If you want to find the chance that an individual has quit by a certain cost, what is that called? ANS 2. Calculate this cost for var when V=1 for costs 0.5, 1.0 and 5x. ANS . Satisfy yourself that the chance of quitting correlates with V in a way that makes sense. Try three values of V, for example 0.5, 1.0 and 2.0? A priori, which should given the lowest cumulative chance of having quit by x=m=1? ANS 4. If P(m) is the cumulative chance that an individual has quit by the time cost x=m is paid, how would you calculate the chance that an individual has not quit by cost x=m? (Note this is not covered on this sheet, but give it a quick whirl.) ANS: |
Endnotes and Answers to Problems
About the abbreviation "dx". Normal notation for this small increment in cost is the lower case Greek symbol for delta x. Apologies, but this is a limitation of HTML -- many browsers will not support symbols in normal text. So when you see "dx" you know that I actually mean the symbol:
|
Back to previous place in text
Answers to the Problems:
1. If you want to find the chance that an individual has quit by a certain cost, what is that called?
ANS: Cumulative probability of quitting by cost x, P(m)
(return to previous place in text)
2. Calculate this cost for var when V=1 for costs 0.5, 1.0 and 5x.
ANS: for x=0.5: P(x) = 1 - exp(-0.5/1) =1 - exp(-0.5)=1 - 0.6065 = 0.3935
for x=1.0: P(x) = 1 - exp(-1.0/1) =1 - exp(-1.0)=1 - 0.368= 0.632
for x=0.5: P(x) = 1 - exp(-2.0/1) =1 - exp(-2.0)=1 - 0.1353 = 0.8647
(return to previous place in text)
3. Satisfy yourself that the chance of quitting correlates with V in a way that makes sense. Try three values of V, for example 0.5, 1.0 and 2.0? A priori, which should given the lowest cumulative chance of having quit by m=1?
ANS: for V=0.5: P(m=1) = 1 - exp(-1/0.5) =1 - exp(-2.0)=1 - 0.1353 = 0.8647
for V=1.0: P(m=1) = 1 - exp(-1.0/1) =1 - exp(-1.0)=1 - 0.368= 0.632
for V=2.0: P(m=1) = 1 - exp(-1/2.0) =1 - exp(-0.5)=1 - 0.6065 = 0.3935
So, we would expect that if the resource was more valuable, an individual would be prepared to pay more which is exactly what this shows. Notice that as V increases, the chance of having quit by cost=m is lower!
(return to previous place in text)
4. If P(m) is the cumulative chance that an individual has quit by the time cost x is paid, how would you calculate the chance that an individual has not quit by cost x? (Note this is not covered on this sheet, but give it a quick whirl).
ANS: It is simply the remaining probability -- thus:
prob. of having quit at x + prob. of not having quit at x = 1.0
(since all probabilities must sum to 1.0)
So, if we define the chance of having not quit as of a certain cost x as Q(m) then
P(m)+Q(m)=1.0
Q(m) = 1- P(m)
so for var, since P(m) = 1 - exp(-m/V) then:
Q(m) = exp(-m/V)
(return to previous place in text)
Copyright © 1999 by Kenneth N. Prestwich
About Fair Use of these materials Last modified 3- 14 - 99 |