Derivation of an Equation that Describes the Maximum Costs of All Supporting Strategies in an Equilibrial Mix for the War of Attrition

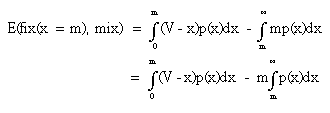
Recall that the reason that we obtained an equation for E(fix(x=m), mix) (eq. 5) was so that we could eventually solve it for a function p(x) which describes the maximum acceptable cost to any pure strategy supporting the mix.

The solution below uses simple calculus; anyone who has had some calculus should be able to follow along. I have tried to include all steps (what Maynard Smith 1974 referred to as "a little manipulation"), even very small ones to avoid confusion (hopefully I have done nothing to create confusion!). If you are not familiar with calculus, it is still worthwhile to get an idea what has been done. The most confusing parts to you will be the values that are substituted into the equations at various points; don't worry about them and just try to get a general idea of what is happening.

We start with eq. 5, the payoff to a fix(x) strategist against the mix. Our first step is simply to re-arrange the second integral by moving the constant m outside:

eq. 5: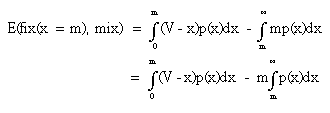

Now, Bishop and Cannings showed that any mixed ESS would have to include all strategies and would be equilibrial (press here to see their proof). That is, E(support strat1, mix) = E(support strat2, mix) = etc = E(mix, mix).

Another way of putting this is to say that the rate of change of payoffs to any supporting strategy fix(any x) against the mix as a whole is zero. In the language of calculus:

and if we substitute eq. 4 we get:

eq. D1: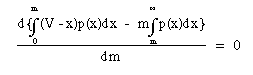

Now since the derivative of an integral is the integrand (the integral's argument) and integrating the second term by parts, we get:

The final expression can be re-written as:

eq. D2:

We need to solve for p(x). Since the derivative of an integral is the integrand, we'll take the derivative of:

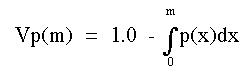
Here are the steps:

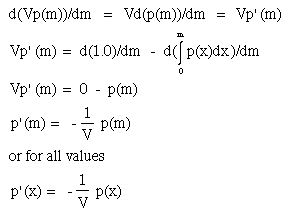
Now, to solve for all values of p(x) we need to integrate the last equation:

eq. D3:

The expressions on the left and right sides of the equation have the following values:

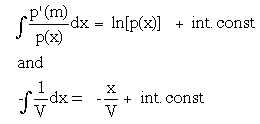
where "int. const" are constants of integration. Substituting these values into eq. D3:

and if we lump the integration constants together we obtain:

eq. D4:

and continuing the solution:

eq. D5:

Now, we would like to know the value of the constant c. To make things simpler, let:

and substitute into the final equation in the previous box and solve for k:

First we get an equation of exponential decay (for more info on these, press here)  We can find k by: now solve for k:

where the final equation is eq. #6, the probability density function.