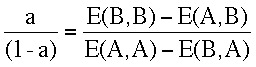
| Synopsis: This page introduces you to the central concept ofthe application of game theory to evolutionary biology -- the EvolutionarilyStable Strategy. You will learn the basic terminology and techniques forsolving evolutionary games with two strategies. After completion of thispage, you will move on to solving a classic two strategy game (Hawks andDoves) and then to simulations and more complex games. |
Why call it game theory? Inthe previous section, (comparingoptimality and game theory), we learned that competition was an importantfeature of game theory (see note). Thus, the analogybetween human behavior and game theory is of competitors (players) seekingto win something through some sort of competition (contest or the game itself).Note that in game theory, as in human games, the outcome of a contest toa particular player is shaped by both the actions of the focal player andher/his opponent. Both human and evolutionary games can have different structures.For instance, the outcome can be determined as the sum of a series of one-on-oneencounters between the players or it can involve to a contest where eachplayer is working more or less against everyone else at once. Clearly inboth of these cases, the outcome will depend on the behavior(s) of the players.
Some Definitions and Caveats
OK, so we understand why these are called games, although from the pointof view of the animals, they are deadly serious. Let's see how we formallyanalyze a game -- how we make theoretical calculations of relative fitnessthat are based on benefits, costs and frequencies of various types of outcomes.
Contests and Games: Let'sget a few conventions out of the way. First, we are only going to look atone general model of competition -- what Maynard Smith termed pairwisecompetition. In pairwise competition each contest involves two individuals ("players") at a timecompeting against each other . Just as importantly, pairwise models viewthe fitness consequences as summing over time (as more contests occur).This type of model is quite useful in animal behavior because there aremany situations where we can see two individuals interacting over some resource.Furthermore, we can see that the consequences of these interactions seemto sum in determining the fitness of the players. (Note: a more common typeof game is probably "playing the field" (see Maynard Smith, 1982) or "n-persongame" by Riechert andHammerstein 1983), but we will not consider this model.
Strategies: The particularbehavior or suite of behaviors that a player uses is termed a strategy(see important note). Strategiescan be behaviors that are on some continuum (e.g., how long to wait or display)or they may represent discrete behavior types (e.g., display, fight, orflee). Sometimes the terms pure strategyand mixed strategy are used. Please do not confuse these with theterms "Pure ESS"and "Mixed ESS"-- it is easy to do. A pure strategy is a strategy that is not definedin terms of other strategies present in the game. Examples of pure strategiesthat we will consider later are "hawk" and "dove" --they represent very different ways of trying to obtain resources -- fightingand displaying. On the other hand, sometimes strategies are mixes of others.An example of a mixed strategy is when one individual plays a mixof "hawk" and "dove" with a certain probability.
About "Mixed Strategies" A mix such as "play hawk sometimes and dove the rest of the time"can also be thought of as a strategy in its own right. Or, it could be givenits own name (e.g., we could name the mix "roadrunner"or whatever). Naming Conventions Used at This Site: On the other hand, if an individual exhibits a mix of pure strategiesbut uses some other condition beyond simple probability to determinewhen to play one or the other of if it adds some additional uniquebehavior, we'll give it its own name. |
As we will see later, pure and mixed strategies are not necessarily ESSs-- just keep all of this in the back of your mind, you'll be reminded aboutit later on!
One more point about "players" (contestants, whatever)and "strategists". Players are individuals who use (play)a specific pure or mixed strategy. When we look at a game, one perspectiveis to consider the fitness consequences of contests on an individual whoplays a certain strategy. However, we will more commonly look at the gamefrom a population viewpoint. The players in a game become the strategiesthemselves (or the genes that encode these strategies). The game will thenconsider the overall fitness effects on each strategy after all possiblecontests are played in proportion to their likelihood. (Trust me, this willmake more sense in a moment). This sort of treatment owes much to populationgenetics where genes (alleles) are commonly viewed in competition with eachother. However, please note that this in no way implies any sort of groupselection -- allele or strategy competition models can be viewed as somethingand its copies (regardless of whether or not these are genes or learnedbehaviors) competing with some other thing (and its copies) where the winnersmake the most additional copies of themselves.
Asexual Models: Finally, to makethe games simple, we assume that the behavior is passed on to offspringby asexual reproduction, or if the behavior is learned that it is simplycopied by the offspring. Thus, there are no complications relating togenetic interactions between the alleles producing different strategies,no need to worry about small population effects etc. Maynard Smith and othershave produced many games where sex is a factor. The interested reader isurged to look at Ch. 4 in Maynard Smith (1982) for an introduction to thesemodels. Notice also that assuming asexual reproduction makes it easy toadapt these models to examine transmission of behavior by learning (assumingthat no modification occurs in the process).
As stated above, when we talk about strategies in the context of pairwisecompetition in game theory, we will be interested in the outcomes of manycontests. Acontest occurs when two individuals interact within the context of the game.That is, they compete for some sort of resource using the behavioral strategiesunder consideration by the game theorist (remember that these games areartificial constructs to allow us to understand what the animals are doing).Contests can occur between individuals that use the same behavioral strategy(e.g., display time 1 vs. display time 1) or they may occurbetween individual with different strategies (e.g., display time 1vs. display time 2).
Let's make this a bit more concrete using the previous example aboutsatellite behavior (to review this example press here). We have two different strategies -- calland satellite (note: these strategiescould be viewed as being either on a continuum of calling or as totallydiscrete behaviors, the distinction is largely semantic in this case).The potential contests are:
What are the evolutionary significances of these contests? Put in theterms of an evolutionary game, we would like to know the fitness (or somestand-in for fitness) consequences on the actors of each type of contest.We usually refer to these fitness consequences as payoffs.
In games involving non-continuous behavioral strategies (review)we usually start with the construction of a payoff matrix. This matrixlists all the possible contests and their associated payoffs. Clickingon the notation for an individual payoff will bring up a window that remindsyou what the payoff is (try it):
Opponent | ||
| Focal Strategy | Call | Satellite |
Call | E(C,C) | E(C,S) |
Satellite | E(S,C) | E(S,S) |
There is a formalism to its construction:
Here's the same matrix again (just to keep it visible!):
Opponent | ||
| Focal Strategy | Call | Satellite |
Call | E(C,C) | E(C,S) |
Satellite | E(S,C) | E(S,S) |
| ! Important: Notice that the payoff matrix is a bit more complicatedthan was the simple list of contests. In the caller vs. satellite game therewere three general types of contests (review), butthe payoff matrix lists four payoffs. Why is this? The reason is that thepayoff matrix lists the consequences to a strategy for each possible typeof contest. It thus becomes obvious that the strategy "call" experiencesa certain type of payoff whenever two callers compete (E(C,C)) and alsowhenever a caller competes against a satellite (E(C, S)). Likewise, thestrategy satellite experiences one type of payoff when pitted against call(E(S,C)) and another when pitted against another satellite (E(S,S)). |
Formal Analysis of a Game
Part 2: Calculating Payoffs to a Strategyin a Particular Contest
Now, lets see how to calculate eachpayoff (see additional fussy notes)
Thus, all payoff calculations will have the general form:
eq. 1. Payoff(to Strat., when vs. a Strat.)= (Benefit from win) - (Cost from loss) |
Since these are contests, procuring a benefit or paying a cost dependson a number of factors. Thus, we must factor in the chance of winning aresource of some value and the chance of paying a cost in losing. So weexpand eq. 1 to:
2. Payoff(to Strat., when vs. a Strat.) = {(chance of win) * resource value} + {(chance of loss) * cost of loss} |
Even eq. 2 (above) is probably not sufficientsince eq. 2 states that winning has no costs. However, in many conteststhere is a cost paid by the winner: Good examples might be energetic ortime costs of displays; these can be seen as lowering the value of winning.Thus, eq. 2 might be expanded to:
3. Payoff(to Strat., when vs. a Strat.) = {(chance of win) * (resource value - cost of win)} + {(chance of loss) * cost of loss} |
We now have a good generalized equation.
| Notice that any of the terms in eq. 3 can be made to drop out simplyby setting them to zero. Thus, in a particular type of contest if the strategyunder consideration incurs no cost to winning and there is no chance oflosing (the chance of winning becomes 1.0), then the entire equation forpayoff reduces to the value of the resource. |
Here are a few important considerations aboutcalculations of payoffs
| ! Obviously the effect is the same; the only thing that mattersis that the game theorist is consistent. |
Formal Analysis of a GamePart 3:
Calculation of the Fitness of EachStrategy
Neither the payoffs for a contest (e.g., the value of E(C,C))nor the simple sum of alltypes of payoffs to a strategy (e.g., the payoff row for strategy C -- E(C,C)+ E(C,S) from the matrixabove) will give the fitness of a strategy (denoted as W(C) or W(S)).Recall that in games, fitness also depends on the frequency of otherbehaviors.
| A moment's reflection will reveal that the frequency of each typeof interaction is a vital part of any fitness calculation -- if satellitesare very rare, then the fitness consequences of interacting with a satelliteare relatively small as compared to if they were more common. |
So, the overall fitness consequences to a particular strategist ina particular type of contest, for example a caller vs. caller contestare given as:
eq. 4: Change in W(Strategy) = E(to Strat, vs. Strat) * freq. (encounter) |
where W stands for fitness and E stands for payoff.
Since our example game only considers two strategies (call and satellite),then if we denote the frequency of caller as c and the thefrequency of satellite as s, then:
eq. 5: Frequency of Caller = c; eq. 6: Freq. of Satellite = s = (1 - c) |
Thus, the fitness consequences of this game to call (W(C)) arethe sum of the payoffs for each type of interaction times the frequencyof that interaction:
Fitness of Call Strategy |
= |
Fitness Change Due to Interaction with other Callers |
+ |
Fitness Change Due to Interaction with Satellites |
or
| eq. 7a: W(C) = E(C,C) * c + E(C, S) * s |
More usefully, if we substitute (1 - c) for s:
| eq. 7b: W(C) = E(C,C) * c + E(C, S) * (1 - c) |
A similar calculation can be made for the fitness of satellite:
| eq. 7c: W(S) = E(S,C) * c + E(S,S) * (1 - c) |
| Notice that both of these equations give fitness as some sort of number.One might think that the larger (more positive) the number given by eitherequation, the more successful the strategy in this evolutionary competition.But is that really correct? - here's your question: Isit correct to talk about the fitness of either strategy in isolation --that is, if only one strategy is present in the population, do the "fitnessvalues" calculated by the eqs. above have any real meaning? |
You have now learned the basic formalisms to set up one especially usefultype of game theory simulation. In the next section, we will look at oneof the most important outcomes in evolutionary game theory -- the EvolutionaryStable Strategy (ESS).
One of the most important consequences of game theory is that it canbe used to determine situations where:
In both cases, the result is evolutionary stasis with respectto the behaviors being considered -- there is no change in relative frequencyof strategies over time. These situations are termed Evolutionarily StableStrategies or ESSs. There are two types of ESS:
"PURE" ESS is where one strategytotally out-competes all others. That means that regardless of its frequency,it is always more fit than any known alternative. A strategy that is a pureESSs is IMMUNE TO INVASION BY OTHER KNOWN STRATEGIES. Thus, any alternativethat appears by mutation or immigration will not be able to increase andwill eventually go extinct.
"MIXED" ESS is where two strategiespermanently coexist. For a given set of payoffs, there will be one set offrequencies where this mix is stable. A mixed ESS can be achieved if individualseither:
In either mixed ESS case, at theESS, all individuals have the same fitness regardless of their strategy(another note!).
At any other frequencies there will be fitness differences. For example,if a new individual enters the population (e.g., a new calleror someone who calls 70% and satellites 30% of the time) the fitnessof all individuals with the behavior behavior of the new individual arelower than the alternative.
| ! One note -- as noted above, at a mixed ESS, the purestrategies exist at the frequencies where their fitnesses are equal.It is very important to realize that when strategies have equal fitnesses,it does not mean that they must also be equally frequent in the population!As we will soon see, the frequencies will depend on the payoff matrix. Wewill see a number of examples of mixed ESSs later and you will be able tosimulate them -- but you will seldom find one where the two frequenciesare equal. |
Other Points About ESSs:
In a two strategies game, there will always be a pure or mixed ESS:
A Couple of Notes ! If the preceding paragraphs confuse you, courage mes amis,we'll look at these concepts in more detail below and then you'll have achance to investigate them with the aid of models. ! Note that when we say an ESS (whether mixed or pure) cannotbe invaded we mean that it cannot be invaded by any other known strategy.ESSs are always defined against other known alternative behavioral strategies.An ESS is always potentially vulnerable to any new strategy that might comealong. We will see examples of this when we go from a two to a three strategygame. |
Question Time -- A simple-minded review -- nothingprofound! ? Assume that two alternative strategies make up a mixed ESS atfrequencies of 0.8 for strategy A and 0.2 for strategy B. Furthermore, assumethat all individuals practice both A and B. ? Explain the differences between a pure strategy and pureESS. Between a mixed strategy and a mixed ESS. (ANS) |
Using The Payoff Matrixto Predict a Pure ESS
in Two Strategy Games
In two strategy games it is a relatively simple matter to determine ifone of the strategies is a pure ESS, provided certain very reasonable assumptionsare met. In this section, we will review the procedure for making this determinationand the logic behind this procedure.
Recall that a pure ESS is a strategy that is unbeatable by other knownstrategies. This means that:
If we can show that either of the statements above is true, then we haveshown that the strategy is a pure ESS (either one is fine, they are essentiallyequivalent as far as the mathematics of the game are concerned).
We can use the payoff matrix and a simplifying assumption to make thedetermination. Let's get away from the caller / satellite model and insteaddefine two abstract strategies: A and B (the purpose of thisswitch is simply to get you more familiar with manipulating and using thepayoff matrix).
As always, the matrix lists the relative payoffs to each strategyfor each type of encounter. In this example we will assign a value to eachpayoff. Thus:
Opponent's Strategy | ||
| Focal Strategy | A | B |
A | E(A,A) = 0 | E(A,B) = 1 |
B | E(B,A) = - 0.5 | E(B,B) = 0.5 |
| ? A quick review on notation -- What does E(B,A) stand for(i.e., what does E(B,A) mean; how could you read it as somethingmore than just the notation E(B,A))? (ANS) |
Let's assume that:
What types of interactions occur and how frequent are they?
The most common contests will involve A strategists. Why is thisthe case? The answer is that nearly everyone is an A strategist and meetingsand conflicts with an alternative strategy are directly related to the freq.of that strategy. Thus:
| ! Any B vs. A conflict can also be viewed as an A vs. B conflict!Put another way, such a conflict involves payoffs to both strategies (E(B,A)to strat. B and E(A,B) to strat. A). Notice however, that from the pointof view of A, interactions with B are extremely rare as compared tothose with A. Thus, we will assume that we can ignore the fitness contributionof A vs. B interactions to the overall fitness of strat. A. You willhave a chance to look at this assumption in moredetail further down on this page. |
! A Note of Warning Remember that we are attempting to calculate strategy fitnesses.Thus, we are interested in the frequency of certain types of interactionsfrom the point of view of the strategy. Since we are considering pairwisecontests, the frequencies of each contest from the point of viewof one contestant (strategist) will be equal to the frequency of the opponentin the contest. Sometimes students who are familiar with basic probability and populationbiology assume that the frequency of a particular payoff equals a term ina binomial expansion of the strategy frequencies. For example, if a = freqStrat A and b = freq Strat B, then (a + b)^2 is expanded to predict that:
This sort of formulation is true if one wants to estimate the rateof occurrence of these interactions in the whole population. Butit is not correct when we are only interested in the frequency of interactionsfrom the point of view of a particular strategy! |
? The following simple problems will illustrate the assumptionswe made about the frequency of various contests in our population mainlycomposed of A strategists. Assume that the frequency of strategy A is0.9999.Calculate:
|
Now, if we consult the payoff matrix, we can see how this invasionturns out. In our example:
From the situation we just considered,we can construct a general ruleto determine whether or not a two strategy game contains a pure ESS:
IF: E(A,A)> E(B,A) (themost common encounter for each strategy)
THEN: A IS STABLE vs. B (it is a pure ESS vs. B) sincethe "Equilibrium Property" of ESSs is true
? Write the expression for determining whether or not strategyB is a pure ESS against A. (ANS) ? Using the expression for B vs. A that you just wrote and thematrix above,explain whether or not B is stable against invasion by A. (ANS) |
You may be wondering what would happen if the fitness consequencesof the most common types of interactions are equal, i.e.,
E(A,A) = E(B, A)
Does that mean that neither is stable against the other? Not necessarily.In this one case, there is an additional test that must be performed beforeconcluding whether or not there is a pure ESS.
If there is more than one B invader, there also may be some rare interactionswith payoff E(B,B). Also, in this particular situation, the payoffE(A,B) starts to matter, even though it is still extremely rare. Again,we have refered to this previously as the stability property (
Why now but not before? In the previous example, the A vs. B interactionwas very rare in comparison with the common A vs. A contests. Thus, anyeffects on the overall fitness of A due tointeractions with B were so small as to probably not matter (review related problem). However in the case we arenow considering, E(A,A) = E(B,A). Thus, the common A vs. A conflict confersno relative advantage or disadvantage. (The same logic applies to the mostcommon contest B experiences, B vs. A). So the remaining interactions willdecide whether or not there is a pure ESS.
Thus, if E(A,B) > E(B,B) A must still have an advantage over Band therefore it will be stable!
To review this, consider the following scenario. A population of A strategistsis invaded by a small number of B strategists. In the most common typesof contests for each strategy the payoffs E(A,A) and E(B, A) are equal.Thus, neither strategy is competitively aided or hindered by these contests.However, in the rare contests, A is doing better than B since E(A,B)> E(B,B) and so A will eventually out-compete B.
? What if this second statement is reversed, i.e., E(B,B) > E(A, B)? Does that mean that B is now stable against A? ANS ? If a strategy is not a pure ESS, does that mean that the opposingstrategy is a pure ESS? ANS |
Summary of Rules for Finding a Pure ESS Assumption -- one strategyis very rare compared to the other. In this example, let A be the commonstrategy and we will determine whether or not it is immune from invasionby B. Rule #1: E(A,A)> E(B,A) or if: Rule #2: E(A,A) = E(B, A) and E(A,B) > E(B,B) There is a method that uses rule #1 to find an ESS by inspection of apayoff matrix. Click hereto see how to use this method.
|
!! You may be uneasy aboutrule #1 (equilibrium property). Mathematically you can vaguely imaginecases where E(A,A) is greater than E(B,A) yet A is not stable against B!These situations require more than one B strategy invader so thatall the payoffs might matter. Since more than one invaderis not an unreasonable scenario, you become suspicious that game theoristsare either intellectually shallow or are trying to sweep things under arug. OK, if you are that interested in the potential limitations of rule# 1, then PRESS HERE for a more complete discussion including a generaldiscussion of appropriate simplification in modeling. |
Finding the Equilibrial Frequenciesin a
Mixed ESS for a Two Strategy Game
What if neither strategy is a pure ESS? If there are only twostrategies, then there must be a mixed ESS.
The reason why a mixed ESS is required in this situation is easy to understand.Imagine a situation where neither A nor B is a pure ESS:
So, let's see how to find a mixed ESS mathematically. We will use thissolution in the simulation as an aid in visualizing mixed and pure ESSs:
Let there be two strategies, A and B at respective frequenciesa and b. We have already seen the expressions for calculating the fitnessof each strategy -- for A:
(eq. 7b): W(A) = E(A,A) *a + E(A, B) * b and for B: (eq. 7c): W(B) = E(B,A) * a + E(B,B) * b |
Now, to achieve and equilibrium, the fitnesses must be equal.If not, one strategy will be increasing relative to the other. Thus:
| eq. 8a: W(A) = W(B) |
substituting:
| eq. 8b: E(A,A) *a + E(A, B) * b = E(B,A) * a + E(B,B) * b |
Substituting 1 - a for b and rearranging, we can solvefor the frequency of strategy A where its fitness is equal to B --i.e., for the frequency of A at the mixed ESS:
eq. 9: 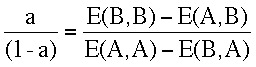
(and we can now use a to find b at the mixed ESS).
This solution can be visualized graphically. If we write both eqs. 7band 7c in the form Y = mX +b where Y is fitness and X is the frequency ofstrategy A, then:
(eq. 10a): W(A) = [E(A,A) - E(A,B)] * a + E(A, B) and (eq. 10b): W(B) = [E(B,A) - E(B,B)] * a + E(B,B) |
If we plots these, we get two straight lines that intersect at some frequencyof strategy A that depends on the values in the payoff matrix. Here is anexample from the Hawks and Doves game that we will look at next. Pleasenote that fitness is being expressed in "payoff units" and beaware that the slopes, intercepts etc. will be different with differentpayoff matrices:
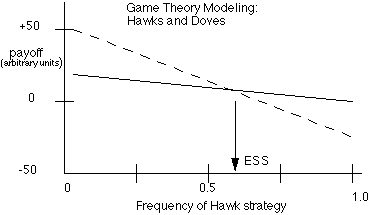
At this point you might expect that whenever two strategies persist ina population then they would always form a mixed ESS. This is not true.They are only a mixed ESS if their fitnesses are equal. You mightask how both strategies could possibly persist in the same population iftheir fitnesses were not equal. What follows is a non-exhaustive list ofrealistic alternatives to a mixed ESS:
Disequilibrium: In a disequilibrium, one strategy is morefit but there has not yet been sufficient time to reach equilibrium. Disequilibriumcould be maintained by a number of processes, for instance the arrival ofmigrants who exhibit the less fit strategy (although presumably it is quitefit in the population they originated from). Genetic drift could also contributeto disequilibrium as could genetic linkages.
Changing Environments: An extension of the idea above.Here, an equilibrium is not reached because the environment changes andfavors one and then the other strategy. There are many examples in evolutionof this sort of cyclical variation and the disequilibrium that results.It has been a hot area of research in population genetics.
"Coping" or "Making the Bestof the Situation" : Let's say that a certain strategy is apure ESS. And let's say that animals have a choice about whether or notto exhibit this strategy. One might think that an animal would always exhibitthe pure ESS strategy, but this is not necessarily so. What if the strategyis very costly and not likely to succeed for an individual who is in a certaincondition? It may be that the alternative behaviors (to the pure ESS) availableto an individual are of demonstrably lower fitness (e.g., they all yieldlower chances of mating in the present).
Let's illustrate this by returning to the caller -- satellite situation.So far we have treated these two strategies as if they were part of a mixedESS. In fact, some studies of anurans have supported the notion that thefitnesses of caller and satellite are equal. However, what if they werenot equal? If we start with the logical assumption that call is morefit than satellite, then we would expect to see satellite disappear.Or would we? We have already considered that calling is costly. What if,on a particular night, a male did not have sufficient energy to call andhave a good chance of attracting a mate? As long as there was some chancethat satellites gain mates, even if fewer than callers, it would pay a "weak"male to satellite or engage in some other less energetically expensive wayto obtain a mate (e.g., searching). Satellite behavior would not disappearbut would remain at a low frequency and would tend to be practiced by individualswhen their energy reserves were low. When they were in better condition,they could call. But even though both strategies persist, they are not amixed ESS.
Another way to look at this sort of coping behavior is as an optimizationproblem -- will engaging in lower fitness behavior give me some gain nowand perhaps even greater gains later thereby increasing my lifetime fitness?
| Testing these ideas: In all of these cases, a decision aboutwhether or not the behaviors were an ESS would require data on relativefitness and their persistence over a number of generations. The importantthing to realize is that simply finding alternative strategies in a populationdoes not prove that a mixed ESS exists anymore than finding a single strategyproves a pure ESS. |
OK, you are now familiar with the basics of pairwise games. We will nowmove onto a series of simple games that will help you to understand howgames work, their implications for behavior, and perhaps also help you seehow to apply abstract games to the behaviors of real organisms.
Continueon to the Hawk and Dove Game
About Competition: Obviously, competitionis also involved at some level in optimality models. Animals that "discover"the best way to perform a particular behavior in situations where the payoffsare frequency-independent are still competing with others, albeithighly indirectly. Perhaps a good way to think about competition in thesense it is used in game theory is that the competition is more direct.It involves something that we might analogize to human contests, althoughthose contests could be the either one-on-one affairs we usually think ofas competition or one against everyone else ("playing the field")
Return to previous place in text
Note that in evolutionary studies, the word "strategy"does not imply conscious choice or planning on the part of the actor.We use the term as a shorthand (in terms of our own experience) todescribe what is happening . But we are aware that in most cases the animalis behaving by some instinctual, heritable rules for behavior -- thus thestrategy is not planned in the sense that a human strategy is planned.
Return to previous place in text
About Payoffs to Strategies and Strategists:One can just as well think about this in terms of payoffs to the strategy(or the strategy's gene) -- but no group selection is implied).
Return to previous place in text
More fussy notes about payoffs: Realizethat payoffs are given as exact amounts in this game when in fact they areaverages; likewise chances of victory are averages -- in a real situationsome animals would clearly be more competent in competitions than others.But we want to keep this simple.
Returnto previous place in text
About fitness: Remember that all of thesediscussions only relate to the traits under consideration in the game. Notall the individuals have the same overall fitness, but these differencesare not correlated with the strategies being considered. And so at thisequilibrium there is no difference in fitness between the two strategiesand therefore no change in either of their frequencies.
I guess it should be mentioned that if both strategiessomehow always have exactly the same fitness, then a situation has beenproduced where change is possible through mutation or migration (or in non-geneticmodels, learning). Notice that this would not be an ESS since the changeswould not cause fitnesses to differ and thereby favor a shift back to theprevious frequencies.
Return to previous place in text
Assume that the frequency of strategy A is0.9999.
Calculate:
the freq. of strategy B : B = 1.0 - a = 1.0 - 0.9999 =0.0001
the frequency of A vs. A interactions
Overall, in the entire population, = a^2 = 0.9999^2 = 0.9998
From the point of view of an Astrategist = a = 0.9999
the frequency of B vs. B interactions
Overall, in the entire population = b^2 = 0.0001^2 = 0.00000001(1e-8)
From the point of view of a B strategist = b = 0.0001
the frequency of A vs. B interactions
wherethe payoff is to A - i.e., E(A,B) = a * b = 0.9999 * 0.0001 = 0.0000999
the frequency of B vs. A interactions
wherethe payoff is to B -- i.e., E(B,A) = b * a = 0.9999 * 0.0001 = 0.0000999
Return to previous place in text
From the last two calculations above, you can see that the total frequencyof those payoffs in the entire population is equal. But that is not whatmatters when considering whether or not A or B are pure strategies. We needto know how common each particular interaction is. And that is simply givenby the frequency of the strategy with which the focal strategy interacts.OK, let's see what this means:
For payoffs to A: 99.99% of them will be with other A strategistsand 0.01% will be with B strategists. Thus, 9999X more interactions willoccur against A; the B interactions would not seem to be very important.
For payoffs to B: once again, 99.99% of them will be withother A strategists and 0.01% will be with B strategists.
Thus, the important payoffs for calculating the fitness of A and B respectivelywhen B is rare are E(A,A) and E(B,A) which account for 99.99% of the interactionsfor both strategists!
Return to previous place in text
Go to:
Copyright © 1999 by Kenneth N. Prestwich About FairUse of these materials Last modified 12 - 01 - 2009 |