Review of the Calculation of Costs to fixed strategists: Recall that all individuals playing a fixed cost strategy have "decided" before the contest as to the maximum amount that they will payout in display costs. If their opponent does not quit at the time that that fixed amount is reached, then they lose the amount equal to their fixed strategy. If their opponent quits first, they lose what their opponent was willing to pay.

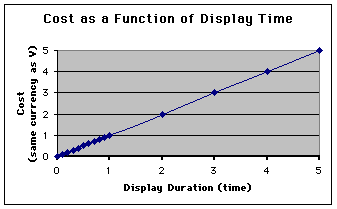
Now, we have assumed throughout this discussion that costs are a linear function of time:

eq. 2: m = x = k * t

where m or x have the same units as V (and therefore the constant k has units of V / t).

Here is a plot of eq. 4 for all costs (m or x ) between 0 and 5 where k = 1:

Note that this graph can be viewed as either:

• the cost that any fix(x) strategist is willing to pay (up to with a maximum duration of 5 )
• or the accumulation of costs (m) for an individual (or for a population of individuals) as it (they) display(s) from t = 0 up to any time t.

Recall that if both contestants select the same maximum cost Maynard Smith stipulated that the winner will be determined at random. Thus, each contestant would win 50% of the time. In every contest both the winner and loser will pay the cost m(A) = m(B).

m(A) = m(B), Therefore, stalemate. Resource possession is decided at random so each wins half of the time.

0.5*V - m(B) (equivalent expression is 0.5*V- m(A))

0.5*V - m(B) (equivalent expression is 0.5*V - m(A))

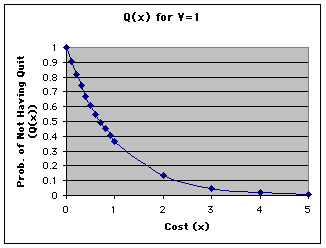
Plot of the chance of still remaining after a certain cost x has been paid:

Payoffs for different contests between fix(x) strategists. In the present context, we are interested in the tie where m(a)=m(b) (bottom row):

Strategy and Outcome	Change in fitness for player A	Change in fitness for player B
m(A)> m(B), therefore A wins	V - m(B)	- m(B)
m(A) < m(B), therefore B wins	- m(A)	V  - m(A)
m(A) = m(B), Therefore, stalemate. Resource possession is decided at random so each wins half of the time.	0.5*V - m(B) (equivalent expression is 0.5*V- m(A))	0.5*V - m(B) (equivalent expression is 0.5*V - m(A))

Hopefully, this table makes sense to you.

• Each row corresponds to the payoffs for players A (yellow) and B (blue) for a given cost (length of display times) that the contestants are willing to pay.
  • Thus, in the first row strategy A is willing to pay more (display longer). A will win every contest.
  • The cost that it and B pay in winning is determined by player B, thus, both contestant's costs are -m(B).
• The second row is simply the converse -- here B wins by being willing to display for a longer period of time and now the cost that is paid is what A was willing to pay.
• The third row -- a tie, is the only one with any new tricks in it.
  • What if both strategies A and B pick the same time (cost) to pay?
  • For the sake of simplicity (but not reality as he pointed out), Maynard Smith stipulated that the winner will be determined at random.
  • Thus, each contestant would win 50% of the time. In every contest both the winner and loser will pay the cost m(A) = m(B). Substituting into the formula for assigning payoffs that we learned earlier :

payoff if both display the same = 0.5 * (V - m(A)) - 0.5 * m(A) = 0.5*V - 0.5*m(A) - 0.5*m(A) = 0.5 * V - m(A)

which is the expression given in the table.

? How is the Dove vs Dove strategy that we considered earlier simply a specific example from this plot?

Answer: The yellow line is the general payoff line for Dove vs. Dove. Notice that the yellow line takes into account all possible costs of this contest. However, in the Hawk and Dove game we simply considered the situation where the resource was valued at 50 and the doves all displayed a fixed cost strategy of cost = 10 (ie., a ratio of V to x of 5). Recall that a winning dove gained 50 and paid 10 for a net of 40. When it lost to another dove, it lost 10. Thus the payoff was the chance of a win * (net gain in winning) - cost of loss = 0.5{(50-10)-10}=15. If we simply normalized these values to V=1, then cost = 0.2 and the net gain was 0.5{(1-.2)-.2}=0.4 which is exactly what the plot shows for x=0.2.

Return to the top of this frame