Wars of Attrition

Wars of Attrition, Part 1:
Introduction. Fixed Cost Strategies:

Synopsis: In the games we have considered previously, weexamined strategies that used fighting (i.e., contests that potentiallyinvolved injury) to settle symmetrical contests (e.g., Hawk and sometimesBourgeois). We also considered the strategy Dove (and Bourgeois when itdid not "own") which settled contests with other Doves throughdisplay. In displays there is no chance of injury although therecertainly are costs in terms of energy, time, or risk of being preyed on(injury from a non-contestant). Thus, we can think of a war of attritionas a contest that is settled without any escalation (no chance of injuryfrom direct interaction between the contestants) with the winner being theindividual who is willing to pay the most (essentially via display) to obtainthe resource.
In this section we will look at how simple symmetrical contests betweenindividuals that only display might be settled without resort to fighting.These contests are referred to as "symmetrical wars of attrition".
We will first examine the question of whether or not any fixed cost displaycan be evolutionarily stable. We will show that fixed cost strategists arenot evolutionarily stable. This will lead us to a consideration of a mixedESS solution in the next section.

Introduction

There are situations where fighting does not occur in a contest overa resource. How then could ownership be settled?

One rule would be simply to cooperate: split the encounters. However, this might only seem reasonable when the contestants knew each other and kept track of their contests so that divisions would be equal (fair). This is not something that most animals could or would do (we humans could do this, but what if you were unlikely to ever encounter the same opponent again?). Game theory modeling of cooperative behavior like this can be done using the "prisoner's dilemma" game. What other possibilities are there?
Another solution would be to settle the contest by some asymmetry, usually detectable in a display. However, this sort of settlement probably only works if there was some back- up to the display. Thus, this leaves the chance for escalation. What if the loser (the one with the supposedly inferior display) calls the winner's bluff? So, if we allow asymmetries, we are left with a model that may require fighting either as a result of the inability of the parties to discern the winner of an evenly matched contest or to back up the "honesty" of the winner's display.
Is there another way to decide without resorting to fighting or sharing? One simple and time honored (not to make a joke) solution is a "waiting game" or "war of attrition". We have seen an example of this in "Dove". Recall that Dove strategists settle conflicts either by immediate withdrawal or by non-escalated display contests. Thus, wars of attrition include the means Doves use to settle contests against other Doves (but not against Hawks!). In this section, we will review some of the ideas about settling contests with displays.

About Waiting Games: In a waiting game, the contestant who iswilling to wait the longest wins. Think of the silly, often tragic dramasof people (often poor and desperate) who enter marathon dance contests (didyou ever see the classic movie "They Shoot Horses, Don't They") to win prize money or those who try to win a car by keeping theirhands on it, remaining awake, and standing longer than any other contestant.

War of Attrition Defined: a contest that is settled withoutany escalation (no chance of injury from direct interaction between thecontestants) with the winner being the individual who is willing to paythe most (essentially via display) to obtain the resource.

Such waiting games have also been dubbed "Wars of Attrition"although they do not need to be strictly analogous to the horrible "real"war of attrition where the winning side is the one whose armies, cities,and populations haven't been "unacceptably" decimated. In ouranalysis of wars of attrition, we will be concerned with individuals (actingas proxies for strategies) competing against each other. We will not beinterested in societal or other group competition as in the military concept(although this analysis could also be used with groups). Types of wars ofattrition that are meaningful to a behaviorist include contests that aresettled:

purely by waiting (or some other type of time-dependent display) or
by depletion of resources such as energy. The assumption is usually made that while costs are involved in waiting, injury (in the conventional sense) is not -- animals drop out of contests before they are seriously harmed.

Return to the top of this frame

Currencies for WaitingGames
The fundamental currency of waiting games is, of course, fitness. Butas we discussed earlier, fitness consequences, measured as changes in numbersof grandchildren, are usually hard to assess for simple behaviors such asdisplays (review).
To save time, we use some other function such as net benefit or netvalue (gain after all costs are factored in). Recall that to find thenet value, we need to have some measure of the value of the resource anda measure of the costs associated with competing for the resource. In waitinggames, these costs are absorbed by both the winner and loser.
Costs as time or energy: Obviously, costs and benefits mustbe enumerated the same way; they must have a common currency.
Let's start our consideration with costs. In a waiting game, theonly costs are display costs. Thus, there is no escalation to fightingand no injury.
What are these costs? Anytime an animal is doing one thing, such as displaying,it is not doing something else that might be helping its fitness. The moretime it displays, the less time it might have for looking for food. Theremay also be costs due to exposure -- animals that are displaying are oftenfar more visible to their predators or other potential enemies.
However, we will consider display costs as the extra energy (comparedto doing nothing) that an organism uses to perform the display. Aswas discussed in the section on optimality (review), these costs are usually a function of time.So, we can make the simple assumption that cost and time are related ("timeis money"):
eq. 1.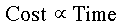
and for our purposes we will assume that costs increase linearly withtime. So:
eq. 2. Costs = x = k * t
where k is a proportionality constant equaling the energy cost(x) of the use of one unit of time (t). A linear relationbetween energy cost and time is probably the general rule in animal repetitiveanimal displays. A good example is calling insects and frogs (see ref). However, note that there are caseswhere cost is not a linear function of time, but we'll keep things simpleand stick with eq. 2.
An example: Let's look at an example of human behavior to understandthe idea of contests and costs. Suppose you are hiking and you are lookingfor a suitable shelter to spend the night. If you arrive at a shelterthat is already occupied either by some critter -- let's say a bear or arattlesnake, or you and another hiker arrive at the same time, acontest starts over who gets the shelter. These contests are settledby displays -- no killings, snakebites or maulings allowed. You tryto scare out the bear or snake while keeping a respectful distance or youdo the typical human things to try to get the other hiker to leave (butlet's not be too human -- no fights!).
Let's focus on the contest with another human since the costs are mostlikely to be symmetrical and since games are usually (but not always) consideredas costs between conspecifics. The cost of the contest is your time andpatience as you discuss or posture over who is going to get to stay.Eventually one you quits. You have both paid the same cost in the contest.And we could have measured this cost either in terms of time or energy (seeeq. 1 above).
Now, what about benefit? Since we measured cost as time or energy,we need a reasonable way to evaluate the shelter in one of these currencies.Assume the shelters are equally spaced in terms of the time it takes toreach them. Occupying a shelter means that you have avoided the cost ofhaving to walk to the next shelter. So in a simplistic but useful sense,the value of a shelter equals the cost you would have paid to hiketo the next shelter. A famous quote from the venerable Ben Franklincrystallizes this idea: "a penny saved is a penny earned".
Avoid the error of thinking about the costs of searching as contestcosts. The costs are only those associated with the actual contest -- theyinvolve the time and energy and perhaps risk involved in giving the "evileye" to the bear, rattlesnake, or other hiker. Search costs are usedonly to obtain a reasonable, easily measured value of the shelter. Noticethat the actual search occurs outside of the contest -- the contest startswhen the search ends.
Return to the top of this frame

Our Central Question: Is therean ESS for a War of Attrition?

To answer this question, we will make the following assumptions(identical to those we assumed for Dove earlier):

We will assume that there are no asymmetries in the contestants beyond the fact that one might be prepared to wait or display longer or, expend more energy (these are all related, as we saw earlier). Thus, animals do not give up because they perceive that their opponent is stronger as a result of the display. So we will refer to these contests as "symmetrical wars of attrition" or symmetrical waiting games.
We will assume that animals have no knowledge of how long their opponents are going to display -- strategies are set at the start of the game and played out.
They simply wait or display up to a certain period of time or burn up to a certain amount of energy.
- If a focal animal's opponent has not yet quit when it reaches its limit, it loses.
- If the opponent quits before the limit is reached, the focal animal wins.
- Since both animals quit at essentially the same time (determined by the loser since the winner is prepared to go on longer), both will pay the same cost in the contest (although for the winner it was less than it was willing to pay).
- This means that the value of the resource is discounted to the winner by the cost of displaying for it. We have discussed this idea earlier when we developed a general formula for determining payoffs in a contest.

For further information on these assumptions, the interested and mathematicallyinclined individual should consult Bishop and Cannings (1978))

The analysis of this game is more mathematically complex than those wehave already considered. The interested reader is advised to consult MaynardSmith (1974 and 1982) and Bishop and Cannings (1978)for elegant, detailed explanations of the problem. What follows is a synopsisof their work with commentary and expansion designed to aid a student whois new to game theory and mathematical modeling. I have tried to make themathematics clear to any student by explaining it fully. There is some calculusin the second section. Nevertheless, students who have not taken calculusshould be able to read and understand the material. And, hopefully theyshould come away with a new appreciation of the use of higher mathematicsin biology.

Return to the top of this frame

Can a Fixed Waiting Time StrategyEver be
a Pure ESS in a Waiting Game?

(i) Costs and Benefits

First, let's define our costs and benefits:

The contested resource has a certain absolute or gross value which we will call V (following Maynard Smith). Since I like to think of things in terms of energy, let's say that it is a certain value in joules.
We will use two symbols for cost.
- Any cost is symbolized as x. These accumulate according to some function of time (see eq. 3 immediately below)
- The cost that each contestant has paid at the moment the contest ends is m. This cost is determined by the loser, but both pay it.
We will assume that display costs, x, increase in a linear manner:

 Eq. 3: x = Display Costs = k * t

Look Out! -- Following MaynardSmith, we will consider costs as positive values and subtract them fromthe gross resource value. This is a different convention then we used inthe Hawks, Doves, and Bourgeois games but the final mathematics are thesame.

Thus, if we have two contestants, A and B who are willing to display for times t(A) and t(B), then we can define their display costs as:

Eq. 4a: x(A) = k * t(A)

and

Eq. 4b: x(B) = k * t(B)

The gain to the winner of any contest will be the value of the resourceV diminished by the cost of getting it. Remember that we will symbolizethe cumulative cost paid at the termination of the contest as m (review the contest):

Eq. 5: Net Gain = V - m

(review the note aboutsign conventions)

Now, recall that the loser pays the same display cost as the winner (sincethe loser determines when the contest will end, i.e., his x when he quits= m -- review)and so the loser pays:

Eq. 6: Loss = - m

(if necessary, review the note about sign conventions)

Return to the top of this frame

(ii) Payoffs:

We can now construct a list of payoffs for different contests.This is not the same as the payoff matrices we have seen before, but wecan use the information on it to construct similar matrices a bit later

Strategy and Outcome
Change in fitness for player A
Change in fitness for player B
m(A)> m(B), therefore
A wins
V - m(B)
- m(B)
m(A) < m(B), thereforeB wins
- m(A)
V - m(A)
m(A) = m(B),Therefore, stalemate. Resource possession is decidedat random so each wins half of the time.
0.5*V - m(B)
(equivalent expression
is 0.5*V- m(A))
0.5*V - m(B)
(equivalent expression
is 0.5*V - m(A))

Hopefully, this table makes sense to you.

Each row corresponds to the payoffs for players A (yellow) and B (blue) for a given cost (length of display times) that the contestants are willing to pay.
- Thus, in the first row strategy A is willing to pay more (display longer). A will win every contest.
- The cost that it and B pay in winning is determined by player B, thus, both contestant's costs are -m(B).
The second row is simply the converse -- here B wins by being willing to display for a longer period of time and now the cost that is paid is what A was willing to pay.
The third row -- a tie, is the only one with any new tricks in it.
- What if both strategies A and B pick the same time (cost) to pay?
- For the sake of simplicity (but not reality as he pointed out), Maynard Smith stipulated that the winner will be determined at random.
- Thus, each contestant would win 50% of the time. In every contest both the winner and loser will pay the cost m(A) = m(B). Substituting into the formula for assigning payoffs that we learned earlier :

payoff if both display the same = 0.5 * (V - m(A)) - 0.5 *m(A)
= 0.5*V - 0.5*m(A) - 0.5*m(A)
= 0.5 * V - m(A)

which is the expression given in the table.

Return to the top of this frame

(iii) Analysis of a Game Between FixedCost Strategies

OK, let's use the payoff matrix to see if a certain strategy is a pureESS. We will use our usual procedure of assuming that one strategy is establishedand the other invades in very low numbers.

Situation 1: An invader willing to pay more arrives!

Define two strategies, A and B
Let B be willing to pay a slightly higher cost than A, i.e.,

eq. 7: m(B) = m(A) + dm

where dm is the small additional cost that B is willing to pay.Thus:

eq. 8: m(B) > m(A)

Make A the common strategy and B a rare invader. Notice that this is exactly the same scenario we have always discussed in determining whether or not a strategy is a pure ESS (press here to review). Thus:
- Nearly all of Strategy A's interactions are with other A strategists while
- Nearly if not all of strategy B's interactions are with A strategists

Let's construct a payoff matrix using the formulae we saw in the table above

A
B
A
0.5*V - m(A) -m(A)
B
V - m(A) 0.5*V - m(B)

Before answering our question about whether or not A can be invaded,let's be sure that we understand the payoffs in this matrix:

When either A meets A or B meets B, contests are settled at random since both contestants are willing to pay either m(A) (if strat. A) or m(B) (if strat. B) -- see last row of payoff table
B always beats A in their contests, thus, E(A,B) = -m(A) and E(B,A) is given in row 2 of the payoff table

Using rule #1for finding a pure ESS, we see than A cannot resist invasion by B and thereforeA is not a pure ESS

Looking at the matrix above, you may briefly be tempted to conclude thatB is an ESS. But look closer:

Situation 2: Same old same old: An invader willing to paymore arrives!

OK, assume that B has taken over and is very common. Nowthe big question:

? What if another strategy (we'll call it C) that waits justa bit longer than B shows up?

The answer, of course, is that we will have a repeat of the situationwhen B invaded A! Thus, C will now successfully invade B and so B isnot a pure ESS.

If you continue to follow this logic, you may come to the conclusionthat a strategy that is willing to pay an infinite cost would be a pureESS. Not so fast:

Situation 3:These Queues are Getting Too Long!

Imagine that our population continues to be invaded by individuals thatare willing to wait longer to win. According to equation 3, the costs are increasing with longer waits,but the value of the resource is still the same. Thus, the net gain forwinning is becoming less and less the longer one waits to win.

Imagine that we finally get to a waiting time that is so long thatit is greater than 1/2 the value of the resource, i.e.:

eq. 9: m(Long) > 0.5*V

Now, this is still a winning value with respect to taking the resourcecompared to any time that is shorter than it is. Let's say a new mutantappears that does not wait or display at all.

? Answer these questions before going on:
1. Construct a payoff matrix for a game of long wait (where m(Long Wait)> 0.5 * V) vs. no display. Explain how you worked out each payoff, referringto the payofftable above when appropriate.
2. Explain whether E(Long, Long) will be a positive or negative number.
ANSWERS

Here's a version of the payoff matrix that you should have gotten:

Long
No Display
Long
< 0 (negative) V
No Display
0 0.5 * V

OK, now if Long represents a strategy where display times are more costlythan 0.5 V, will it be stable against invasion by individuals who simplydo not display?

Once again, Long is common, No Display is rare.
Looking down the first column which shows the most common interactions for each strategy, we can see that No Display can invade once the displays get costly (long) enough.
One other point about No Display. Notice that if 0.5 V>m(Display), then the matrix looks like this:

Long
No Display
Long
> 0 (positive) V
No Display
0 0.5 * V

and a population of No Display can be invaded!

! Conclusions: This exercise has shown us that there is nopure ESS in the waiting game. We have seen that no displays can be invadedby increasingly more lengthy (costly) displays until the point where thecost of the display exceeds 0.5, the resource value at which point no displaycan invade again!

Rock Paper Scissors
It is often pointed out that the outcome we have just seen has certainsimilarities to the child's game Rock Paper Scissors. Recall thatin that game (which you may have played) there are three pure strategies(rock, paper or scissors). Here are their definitions:
Rock breaks Scissors: E(R,S) = +1, E(S,R) = -1, E(R,R) = 0
Scissors cuts Paper: E(S,P) = +1, E(P,S) = -1, E(S,S) = 0
Paper covers Rock: E(P,R) = +1, E(R,P) = -1, E(P,P) = 0
So the payoff matrix is:
Rock Scissors Paper
Rock 0 +1 -1
Scissors -1 0 +1
Paper +1 -1 0
As with the waiting times we have just investigated, clearly none ofthese strategies are pure ESSs (use the "look down the column" rule).
Do you remember (from your childhood) the best way to win or at leastsurvive in this game? We'll come to it in a moment.

Return to the top of this frame

A Mixed ESS Solution to theWaiting Game

So, how about our "war of attrition" game? From theprevious section it should be clear to you that there are situations whereany "pure waiting time" (pure strategy) can beat any other. Thus,there is no pure ESS solution to the war of attrition. However, couldthere be a mixed ESS?

To over-view the answer to this question, let's start out with the Rock Paper Scissors game. Its solution willhave some parallels the one for our war of attrition which we will see onthe next page. But it will also have one very important difference, whichwe will explain in the next section. Nevertheless, let's continue withRock, Scissors, Paper.

If you played Rock Scissors Paper as a child, you may remember that youcould not win if your opponents knew which strategy you were going to pick.For example, if you pick Rock consistently, all your opponent would needto do is pick Paper and s/he would win. A child discovers quickly that ifshe or he doesn't know what the opponent will pick, then the best strategyis to pick Rock, Paper or Scissors at random. In other words, the playerselects Rock, Paper or Scissors with a probability of 0.33.

It should be obvious that if you do know what your opponent islikely to do, then picking a strategy at random with a probability of0.33 is not be the best thing to do (unless that is the strategy they areusing!). This was probably how you consistently beat inexperienced youngerplayers (who tend to employ the same pure strategy repeatedly until theycatch on).

If you played the "play R, S, or P with a probability of 0.33"strategy as a child, you may remember that when you played the game againstanother savvy player, you only won half the time. But the other player didnot win any more often and if someone else tried a different strategy, heor she did not do as well.

? What is the game theory term that can be applied to the strategy"play either Rock, Paper, or Scissors at random with a probabilityof 33.3% in each game"? ANS

Now back to our waiting game. Unlike Rock Scissors Paper, potentiallythere are an infinite number of pure strategies (each a different waitingtime) instead of just three. Nevertheless, in the next section we willsee that the solution has one important parallel to Rock, Scissors, Paperin that the solution requires a mixed strategy.

Go to the nextsection dealing with mixed strategies and the war of attrition

Return to the top of this frame

Strategy and Outcome	Change in fitness for player A	Change in fitness for player B
m(A)> m(B), therefore A wins	V - m(B)	- m(B)
m(A) < m(B), thereforeB wins	- m(A)	V - m(A)
m(A) = m(B),Therefore, stalemate. Resource possession is decidedat random so each wins half of the time.	*0.5V - m*(B) (equivalent expression is 0.5V- m(A))	*0.5V - m*(B) (equivalent expression is 0.5V - m(A))