Synopsis: This page will show that a particular mixed strategythat is composed of all possible acceptable costs, each to be played ata unique frequency is evolutionarily stable in the symmetrical war of attritionagainst any pure strategy (unique maximum cost) or other mix of pure strategies.We will term the stable mixed strategy "var". We will seethat var is characterized by:
The approach on this page will be to
Please note that this is the most mathematical sectionof the Game Theory Website. It must be so because we will need to derivean equation that describes potentially an infinite number of behaviors (aninfinite number of different maximum acceptable costs). In finding thisequation and later in showing that 'var' is an ESS, we will makeuse of simple differential and integral calculus. I have tried to explainwhy these techniques are used and further, to explain how they are usedso that any interested student, regardless of whether or not they are familiarwith calculus, should be able to follow the arguments. As importantly, Ihope to convince students of the benefits to any biologist gained by understandingbasic calculus. |
| Note: In addition to the hypertext, Prof. Kevin Mitchell ofHobart and William Smith Colleges has provided an excellent overview of integration and probability density functions.This is available as a PDFdocument. |
On the last page we learned that in the symmetrical war of attrition,each unique cost x that an animal is prepared to pay (or time itis willing to display) is a pure strategy. Thus, there are potentiallyan infinite number of pure strategies each defined by a different cost x.
We also learned that no pure strategy is an ESS in the war of attrition.Given this, could there be a mixed ESS?
In looking for this mixed ESS, we must realize that any pure strategyis a candidate for inclusion in the mixed ESS. In fact, we expect thatevery possible pure strategy should belong to the mix (i.e.,all possible maximum acceptable costs should support the mix). The reasonfor this is simple -- we learned earlier that under the right circumstances,any fix(cost) strategy can increase and/or mixes of these strategies canappear -- it's just that none of these are evolutionarily stable. So,we expect that any stable mix will contain all possible strategies as supportingstrategies. Presshere to review and to get a glimpse of the ESS we pursue!
Definitions: PURE STRATEGY is defined as some unique maximum acceptablecost between zero and infinity. SUPPORTING STRATEGIES: all pure strategies that are members ofan equilibrial mix. See Bishopand Cannings (1978). A synonym for supporting strategy is componentstrategy. |
In characterizing a mix, we must know the likelihood that a givenplayer might encounter each of these supporting strategies. While itis possible that these frequencies are the same for each supporting strategy,it would seem far more likely that many if not all supporting strategieswould occur at their own unique frequencies. The only rules are that:
Thus, we can summarize the mix as:
| eq. 1: |
where a, b to n are supporting strategies and prob(cost(a)),etc. is either the frequency of the strategy in the population orthe probability that a mixed strategist "adopts" that particularcost in a given contest.
Notice the last point -- as we learned earlier when we considered the"Hawks and Doves" game, there are two ways to produce an equilibrialmix. To this list, we'll add a third. A populationthat is evolutionarily stable could be:
As we start to look for a way to describe the mix, we seem to face adaunting task. We expect all possible costs to be members of this mix. Thus,there are an infinite number of supporting strategies each potentiallyat its own unique frequency.
So, we will not be able to use the simple technique to find the mix thatwe learned with Hawks and Doves. Instead of only needing a couple of linearequations to find two frequencies, we need a function that can give usthe correct frequency for an infinite number of different supporting strategies!What follows is a general description of the methods used by Maynard Smith(1974) to find this function.
| Please read this section carefully; it sets the foundation, establishesterminology, and reviews the mathematics used throughout the rest of ourtreatment of the war of attrition. Exposition that is not crucial (i.e.,can be taken on faith) is located on supplementary pages. Follow links tothese pages when you are confident of the basics -- they're worth lookingat, when you are ready. |
Here we go. We shall use the payoff that a specific supporting strategyexpects to receive when competing against the 'mix' to find the functionthat gives us the equilibrial frequency of each strategy supporting themix.
So, we start with a pure strategy that is a member of the mix. (See aboveto review why a pure strategy can be part of the equilibrialmix.)
Now, imagine that fix(x=m) is about to play a series of contests atrandom against other individuals (supporting strategies) from that mix.So, fix(x=m)'s opponent in any contest can be understood to be "mix"itself.
| Remember, it doesn't matter whether fix(x=m)'s opponent is a pure ormixed strategist: in either case we know the result is that onlyone strategy can be played by an opponent in a given game and the chancethat a particular strategy (maximum cost) will be faced is given by thecharacteristics of the equilibrium (review). |
Let's find an equation for the payoff fix(x=m) receives againstany other supporting strategy in the mix, E(fix(x=m), mix). Starting,in general terms:
Lifetime Net Benefits to Focal Strategy in Wins Minus Lifetime Costs to Focal Strategy in Losses
|
In finding these equations, let's make one other important assumption-- we will assume that the resource has a constant value in any givencontest.
Constant Resource Values? You may think that it is obvious that a resource value should be constantin any contest. There certainly are many if not most situations where thisis true. But, think for a moment and you'll realize that it is quite possiblefor a resource to become depleted during a contest. For example, individualsmay be contesting a resource that one of them already is using or that naturallydepletes in value over time independent of anything the contestants aredoing. Or, while two individuals contest for a resource, it is possiblethat another individual, perhaps a member of a different species depletesit. So, while reasonable for most situations, the assumption that for acontest V= constant may not always be justified. |
Finding Expected Lifetime Net Benefits: Benefitsare only obtained by the focal strategist when she wins -- i.e.,when the focal strategist is willing to pay a higher cost than her opponentfrom the mix (x < m where m = the cost the focal strategistwill pay):
| eq. #3a: Net Benefit to fix(x=m) in a win = (V - x) |
where V is the resource value and x is the cost the opponentfrom "mix" is willing to pay.
Unfortunately, equation #3a is not sufficient for our needs. Thecomplexity of the war of attrition intervenes!
Recall that the mix is composed of an infinite number of componentstrategies. Fix(x=m) only faces one of these supporting strategies inany given contest. Thus, equation #3a only describes the net gain in onespecific contest. You should realize that this particular contest will probablybe quite rare given the many different strategists that fix(x) could facefrom the mix. Thus, one particular contest and its benefits will have littleif any important lifetime effect on fix(x=m)'s fitness. Singlecontests cannot describe the net benefit that the focal supporting strategyexpects to gain from a large number (a lifetime) of contests.
To get an accurate measurement of lifetime net gains, we need to takeinto account all types (costs) of contests that fix(x=m) will win and theprobability of each:
(If you are having any trouble with this, please press here and read some more.)
Let's re-express eq. 3b using the notation of calculus (If youaren't familiar with calculus, don't fret because it will be fully explained!).We will use calculus because it will let us solve this complex problem (algebrajust won't work here) and because it will ultimately give us an exact answer.
First, the definitions of a number of symbols (most we have seen before):
and to reiterate:
Equationfor Net Benefit to Focal Supporting Strategy Now, for those of you who haven't had calculus or who need a review,let's see what eq 3c means. First off, realize that it expresses the sameideas as does eq. 3b. With that assurance, let's start with the expressionto the right of the integration sign (the integration sign is theS-like symbol with m above and 0 below it -- moreabout it below):
This expression calculates the lifetime net benefit in winning a contestof a given cost x. Recall that V = resourcevalue and that x is the maximum cost that aparticular opponent is willing to pay. Thus, as in eq. 3a, (V - x) is the net gain to fix(x=m)(see below for note about wins). For example,if in a given contest V = 1.0 and x = 0.001 fitness units, the net gainin winning this contest is 0.999 fitness units. Note that we couldjust as well write(V-x) as (V-m) and we will later on. Remember that it is not certain that fix(x=m) will play any particularsupporting strategy in the mix. Instead, the probability of playing againsta particular strategy x supporting the mix is p(x)dx wherep(x) is the function that we want to discover to complete the descriptionof the mix. The notation dx that follows p(x) simply meansthat we will multiply p(x) times an infinitesimally small value of cost.So, solving p(x)dx will give us the chance that our focal fix(x=m)strategist faces any particular value of x from the mix.Be careful notto assume this means some variable "d" times the cost x that"mix"adopted in this game. Also, don't make the common mistake of thinking thatdx increases as x increases. It is a constant, tiny amount of cost. Finally, there is the integration sign:
Notice how the limits of the integration arecrucial for defining what is a victory by fix(x=m) over mix. As longas the x from the opposing "mix" is less than m, then fix(x=m)wins and the expression calculates the added lifetime net benefit of thiswin. To summarize: for any contest where x < m, we
|
Expected Lifetime Costs for Losses: Benefitswere the hard part of the E(focal supporting strategist, mix) equation.Calculation of lifetime costs to focal strat fix(x=m) in contests itloses to the mix (i.e., a mix strategy opponent) is much easier.
As before, the logic is simple. Fix(x=m) loses whenever x, the cost theopponent from mix in any particular contest is willing to pay, is greaterthan m. All of these contests end with a cost = m. Therefore, forany one losing contest:
So, unlike the equation for net benefit, the costs in any loss are alwaysthe same. But, we're not done because as with net benefits, we need to takeinto account the proportion of the time fix(x=m) encounters an opponentthat (in this case) it loses to:
Lifetime Costs of Losing to the Mix where m is the maximum cost that our focal supporting strategywill pay and the function Q(m) gives the lifetime proportion of timesthat fix(x=m) loses to another member of the mix. Now:
Once again, some explanation of this equation:
To recapitulate, to get lifetime expected cost of losses, we simply multiplythis cost times the chance that fix(x=m) will lose. Notice that as with net benefits, the function p(x) is central.
|
So, to get the expected lifetime payoff to fix(x=m)vs. the equilibrial mix, we simply substitute the two equations fornet benefit and cost:
|
Now we have the payoff equation (eq. #5 ) that contains the function p(x). How doesone solve to find the function p(x)? It is not terribly difficultbut then neither is it central to our story. At some point, if you are interested,you should take a look. But for the moment, we'll proceed directly to thenext section where we'll introduce the result that Maynard Smith obtainedfor p(x) and we'll discuss it in considerable detail.
Presshere to view an outline of how the solution of eq. 5 for p(x) is found. |
Recall that Maynard Smith's goal was to find a function, p(x),that would supply the frequencies of each supporting strategy (cost, x) for an equilibriumin the war of attrition. To get p(x) he solved eq. 5 and obtained the following result:
where p(x) is the probability densityfunction (dimensions of probability per unit cost), xis cost, V is resource value ande is the base of the system of natural logarithms(e about equals +2.713). We will also write this expression as 1/V*exp(-x/V) where exp(-x/V) isthe same thing as writing e to the negative (x/V). Important note: Remember that exp(-x/V) is the equivalent of 1/exp(x/V).Negative exponents are the same thing as the inverse of the expression.So 2^ -2 = 1/2^2 = 1/4! |
Eq. #6 is an example of type of function called a probabilitydensity function.
Negative exponential distributions are an example of a very importantgroup of functions called Poisson distributions. |
However, it does not give frequencies of different maximum acceptablecosts. Instead, true to its name, it gives probability density: probabilityper unit x. To make this a bit more concrete, solutions to eq. #6 giveprobability (or frequency) per unit cost.
Another Note -- Probabilities and Frequencies: I was not pullinga fast one when I equated probabilities and frequencies. A quick review-- remember that a frequency is simply the proportion of the total madeup by one particular class. For example, if 20 out of 1000 in a war of attritionwill pay a cost of up to 0.08 fitness units, the frequency of individualspaying a maximum cost of 0.08 is 0.02 . By the same token, if we were torandomly pick an individual from this population, the chance of pickingan individual who would pay a maximum of 0.08 would be 0.02 (2%). The maindifference in common usage between the terms probability and frequency isthat probabilities are usually theoretically expected proportions whilefrequencies are often actual measured values. However, probability valuesare often used synonymously with expected frequencies in theoretical distributions;that is what we will be doing for the rest of this section. |
How do we get simple probability (frequency)? We need to multiplyp(x) by cost. Now the earlier equations that contained p(x) (e.g.,eq. #5)should make a bit more sense. Notice that they contained the expressionp(x)dx which means to:
A word about probabilities and ranges of cost. Since cost is a continuous variable,for any exact value of cost the frequency of contestants who play that exactvalue is exceptionally low (unless we are dealing with the exceptional caseof p(x)d(x)=1.0 -- also see the grey box above) .Probability accumulates as a continuous variable changes. Thus, thegreater the range of the costs that we consider, the greater thefrequency of individuals between those costs (alternately, the greater theprobability that a mixed strategist will quit between these two costs ina given contest).
As you probably (no pun) know, integration would be the best techniqueto apply to the problem of finding the frequency of individuals willingto pay or not pay a certain cost x. Recall that when we integrate, we invokeproven mathematical techniques that have the effect of adding togetherthe results of solving for p(x)dx at each x(each tiny step). (Actually,the way I just described the process is a bit more like the way a computerwould accomplish this operation, but in any case, it gives you the rightidea about what integration accomplishes.) Thus:
where p(x) is the probability density function(dimensions of probability per unit cost) and dx is a tiny incrementof cost. What eq. #7 says to do is:
To gain a bit more understanding, let's see an example. Let's solve eq.#7 using the rules of integral calculus (if you've taken calculus this willbe familiar, if not, just realize that we apply some rules to get the expectedresult)
Here's a step by step analysis:
Now since:
|
Now you should have the basic idea about how we go from the probabilitydensity function (eq. #6) to probability. Since we're on the subject, let'ssee how we calculate the cumulative (total) probabilities (frequencies)of playing up to or beyond any particular cost (we alluded to thesecalculations earlier when we wrote expressions for net benefit to a supportingstrategist (eq.3c and 4)). Let's also see how to integrate eq. 6 to get an expressionthat tell us the chance that an individual plays up to a certain time.
First, let's find an expression for the totalproportion of individuals in the mix who are expected to have quit betweencosts between zero and cost x=m (this of course is the same as givingthe chance that a mixed strategist will quit by cost m). This is calledthe cumulative probability distribution of quitting times, P(m)
Let's discuss this equation. Upon integrating eq. 8a we get a formula from which we can readily calculateP(m) for any particular cost (x=m): (presshere to see the steps of the integration of eq. 8a) To reiterate: when we solve eq. 8b for any cost, the result willbe the total proportion of a population of mixed strategists who would havequit as of cost m. Again, remember that this does not mean that they allquit at cost m. Instead, P(m) includesthose quitting at cost m AND all that have quit before cost m. Hereare plots of P(m) for three resource values (V) over a range of costs betweenx = 0 and x = 10:
Notice that in all cases the initial chance of having quit is (of course)zero. As contest costs accumulate, it becomes more likely that one willhave quit since costs start to exceed the maximum different supporting strategiesare willing to pay. (Note: we have talked about individuals who quitat cost = 0; assume that what really happens is that they quit after a smallcost, 0 + dx, is paid). Another way to think about these plots is to imagine 1000 identical'mix' strategists starting a display game. At time zero, all are playingso zero have quit. A short time later some have quit, as time goes on agreater and greater proportion have quit and so the overall chance thatan individual who started the game will have quit gradually increases. The other thing to note is the effect of V on quitting. As V getslarger, individuals quit at lesser rate (fewer quit per increase in costx). This should make sense -- a contestant should be less likely to giveup over a valuable resource. In fact, the rate of quitting is proportionalto 1/V; more about this below.
|
Hopefully this is all starting to make a lot of sense. Now let's lookat the converse of the cumulative probability of having quit as cost x=m(alternately -- the total frequency of quitters as of cost x=m). The conversewould be the cumulative frequency who have not quit as of cost m(a.k.a. "probability of not having quit", or the probabilityof enduring to a certain cost); we call this Q(m) and we sawit earlier with the equation for net cost to any supporting strategy vs."mix":
OK, if P(m) is the cumulative chance that an individualwill have quit as some cost, then 1- P(m) will be the chance that theyare still playing. We'll call this Q(m): the probability ofenduring up (not having quit) to a certain cost. Here is a graph forQ(m) when V=1:
We can of course find Q(m) by integrating p(x) from m to infinity.Press here if youwant to see this integration. Now, as with P(m), if we solve eq. #9 for a series of values ofcosts we can get a plot of the cumulative chance of enduring (not quit)as of any cost m. Review the plotfor P(m) and then try to imagine how this graph should look. Afteryou have thought about this, press here to see the plot of Q(m) vs. cost. |
Notice that eqs. 8 and 9 both give us cumulative probabilities.This means that both give frequencies/probabilities starting at zeroup to some cost x=m (thus, if that cost x is infinity, then the cumulativechance of having quit by that cost is 1.0 and the cumulative chance of nothaving quit is 0).
But what if we simply want to know the chancethat an individual will quit over some specific cost range -- for example,between cost x1 = 0.50000 and cost x2 = 0.50001. This is especially usefulin understanding how a computer solves the war of attrition such as inthe war of attrition simulation that accompanies this page.
eq. #10: Calculation of deltaP(x) notice that this is the same expression as:
|
So, we have now gone over the equations that can give us various probabilitiesor frequency distributions in the war of attrition. All of these are the"children" of eq. 6, the probability density function that Maynard Smithderived to describe the mixed ESS. We will use these functions in the discussionsthat come below or on related pages (for instance, we will use eq. 10 on a related page that considers how a computer wouldsolve the war of attrition).
In the next section, we will talk about what eq. 6 really means: whatdoes it say about mixed strategies in the war of attrition. After we havea full description of this mix, we will turn ourselves to our final task-- proving that the mix is an ESS.
QuestionsAbout Chances of Continuing 1. Name the probability distributionsthat we saw earlier that give (i) chances of continuing to a certain costor (ii) quitting as of a certain cost. Answer 2. If eq. 11 gives the chance of continuing for a unit ofcost, write an expression that gives the chance of quitting per unit cost.Answer
|
We are now at a point where we can understand the characteristics ofthe mixed equilibrium. As mentioned previously, this equilibrium could consistof either:
Thus, eq.#6 has a key role in describing the equilibrium.
In this section we will focus on the characteristics of the equilibrium.How should members of a population at this equilibrium act?
Important Convention For convenience we are going to think about our population in terms ofthe second possibility just discussed -- we will regard the equilibrialpopulation as consisting entirely of mixed strategists, all of whom arecapable of playing any maximal cost with a probability ultimately describedby eq. 6. |
Since other mixes are possible we'll give this particular mix a name'var' for variable cost strategist.
A Note About Strategy Names Some of this is reiteration of what was just said but please glance overit so that you are familiar with the strategy names and definitions we willuse from here on out. The names and symbols we will use for the strategies are a bit differentthan those used by Maynard Smithand Bishop and Cannings.They are meant to be more descriptive and therefore easier for someone toremember; hopefully this use will not result in any confusion. to thosefamiliar with these author's work. I do this with some reluctance buthave found that my students seem to have an easier time this way as comparedto using symbols such as I and J or the generic term"mix". So:
|
What are the characteristics of ourmixed strategy "var"?
1. Like other strategies, 'Var' is highly secretive! There can NO INFORMATION TRANSFERfrom var to its opponent THAT MIGHT SIGNAL WHEN 'VAR' WILL QUIT.
2. Varstrategists may potentially play any cost -- from no cost to (theoretically)an infinite cost. We discussed the reasons for this in the first sectionof this page (review).
3. 'Var' strategists have a constant rate of continuingover each unit of cost. The chance of continuing is proportionalto 1/V; this quantity is also known as the rate constant (presshere if you want to reada bit more about rate constants). The chance of continuing perunit cost:
eq. 11: (note that this equation is the same as eq. 9 when Q(m) is solved for x= m = 1) |
Thus, with regard to the chance of var's continuing to display:
If you don't spend a lot of time dealing with exponents, theselast two statements might confuse you. It is very important that you keepin mind the fact that x/V is part of a negative exponent.Thus:
|
4. Now, since the behavior of a 'var' strategist is determinedby a certain chance of quitting with each unit of cost, and since varnever tips its hand, you should realize that an opponent will never knowexactly when a 'var' strategist will quit -- anymore than you, me oranyone can always correctly guess when a "fair" coin will turnup "heads". Thus, knowing when something will happen is quitedifferent from knowing the chance of some event. This is the essence ofthe problem var's opponents face!
5. Another result of a constant chance of continuing per unitcost (i.e., a constant chance of quitting per cost) is that thechance of accepting greater costs (i.e., of playing from the start throughto cost x) decreases exponentially (for any value of V less than infinity,i.e., for any exp(-1/V) < 1.0). The effect of this is that there is virtuallyno chance that a var strategist will be willing to pay a cost thatis very large compared to V.
6. To summarize, the opponent:
Link to an Illustration of "Var - Like" Behavior The last statement is perhaps the most crucial in understanding the behaviorof 'var' strategists. Central to it are the ideas of constant probabilityof continuing the game and independence of decisions from one moment (cost)to the next. You will also explore this in great detail when you run thesimulations. For the moment, however, take the time to read an example illustrating how a strategy like 'var' works. |
Questions About the MixedStrategy Var 1. Compare what a contestant sees when itconfronts a population consisting entirely of 'var' strategists as comparedto a population that is an equilibrial mix of pure supporting fix(x) strategies.Would the contestant see any difference in these two situations? Answer 2. How would you express the idea of constantrate of quitting with respect to a population of pure strategists who togetherproduce an equilibrium? Answer 3. Why is it crucial that no informationas to var's intention to continue or quit a contest be passed onto its opponent? Answer 4. How do you estimate the probabilitythat a var strategist will win a contest of cost x? Answer 5. How do you estimate the probabilitythat a var strategist will lose a contest of cost x? Answer 6. How do you estimate the probabilitythat a var strategist loses by paying a cost between x and x+dx?Answer All of the remaining questions call for solutions to equations derivedfrom eq. 6, the probability density function that describes var. You willneed a calculator or spreadsheet with natural logs. Alternatively, you canuse the number 2.72 whenever you need e. 7. Should the chance of encounteringa member of the "stable mix" with a quitting cost between 0.60and 0.61 be greater or less than encountering an individual with a quittingcost between 0.60 and 0.62? Explain. Answer 8a. What is the chance of encounteringa member of the stable mix with a quitting time between a cost of 0.60 and0.61 if V=1? V=0.5? Compare these answers with the next question. 8b. What is the the chance of encounteringa member of the mix who quits between a cost of 1.0 and 1.01 if V=1? V=0.5?Compare these answers with the last answers. Why the difference? -- thesize of the cost interval is the same Answer. |
We now know the general characteristics of the mixed strategy we call'var' -- the rangeof its maximum display costs, the probability of playing each of these costs,and the relationship of these probabilities to the resource. And we knowthat the equation that eq. #6, which describes var's behavior sprung from theassumption that:
E(any fix, var) = E(any mix, var) = E(var, var) = constant |
Finally, we know that Bishop and Cannings (1978) have showed that thisassumption must correct for any ESS in the symmetrical war of attrition(see Bishop-Cannings theorem).
However, simply showing that the 'var' strategy has some behavior consistentwith being an ESS is not the same thing as showing that it is an ESS. Recallthe two general rules for finding ESSs we learned about earlier .'Var' is an ESS (cannot be invaded if sufficiently common) if:
Now, in the case of 'var' we are only interested in rule #2 sincewe already know that part a of rule #2 is true. In fact,'Var' isderived from part a! And of course rule #2 is not consistent with rule #1.But just because 'var' is derived from rule #2(a) does not mean thatit must be consistent with rule #2(b). And if 'var' vs. any fix(x)is not consistent with part B, then var is not an ESS (see box below).
If 'Var' Were Not an ESS, What Would It Be? If 'var ' vs. any fix(x) is only consistent with rule 2 part A, it isequilibrial. This is because if E(var,fix(x)) > E(fix(x),fix(x))is false, then the only interpretation that is also consistent with rule2A is that E(var,fix(x)) = E(fix(x),fix(x)). So, the common interactionswould have the same fitness consequences on each party (no advantage toeither) and the rare interactions would also give no advantage to eitherstrategy. Note that the payoffs in common vs. rare interactions would nothave to equal each other, the only equality needed is that common are equalfor both as are rare. The result is that selection could not change thestrategy frequencies and we would say that the population was equilibrial.(The only way that frequencies can change are by mutation, immigration oremigration.) |
So, to show that 'var' is an ESS all we need to do is to show thatrule #2 part b holds:
Rule 2, part b: E(mix,fix(x)) > E(fix(x),fix(x)) |
What will follow is a mathematical proof that rule 2b is in fact trueand therefore that 'var' is an ESS in the war of attrition. Once again,there will be a bit of calculus to enhance the argument but anyone shouldat least be able to follow the outline of the proof. As before the calculusis all explained, furthermore, much of it is very similar to what we haveseen earlier. And, to make the concepts clearer, a number of graphs willbe presented.
Once again,'var' is an ESS if:
Rule 2, part b: E(var,fix(x)) > E(fix(x),fix(x)) |
is true.
So, we will need to find expressions for E(var,fix(x)) and E(fix(x),fix(x))and determine whether or not the difference between the two is always apositive number -- i.e.,
| eq. 12: E(mix,fix(x)) - E(fix(x),fix(x)) > 0 |
Now, recall eq. #2 from earlier. The payoff to a given strategy in acertain type of contest is always:
eq. #2: E(focal strat., opponent) = Lifetime Net Benefits to Focal Strategy in Wins |
So, let's find the net benefit and cost equations for E(mix,fix(x))and E(fix(x),fix(x)) and then substitute them into eq. 2 before finallysolving to see if we have an ESS. We'll use the same general symbolsand operations that we used in finding E(fix(x), mix (i.e., 'var')) earlier.
Part One: Calculation ofNet Benefits
The benefits needed to calculate these payoffs are easy to find and sothey represent a good place for us to start. First, recall that we assumethat the value of the resource is constant in any given contest; furtherwe assume that it has the same value to both contestants. As usual,we will symbolize it as V. Here are the net benefits for each typeof interaction.
Net Benefits to Var in Contests vs.Fix(x): Remember that var does not enter a contest possessinga particular maximum cost that it is willing to pay. Instead, at eachinstant it has a constant probability of quitting proportional to 1/V.Thus, it is unpredictable as to exactly when it will quit.
Now remember that in wars of attrition, winners, like losers, paycosts. These costs lower the net (realized) value of the resource tothe winner (press here to reviewour assumptions about costs):. We'll call the maximum cost the fix(x)strategist is willing to pay m). So, against a given fix(x=m)strategist, 'var' wins whenever it is willing to pay more (i.e.,whenever it continues to play after fix(x=m) quits). Thus, when 'var'wins, it will always win V-m. But it is not certain that 'var' will playto a higher (winning) cost than fix(x=m) since var uses a probability functionto determine when to quit. So, 'var' expects to get:
| eq. 3b: net Benefit = (V - m) * (Chance of winning) |
Recall from earlier that the chance that 'var' has not quit as ofpaying any cost x= m is Q(m):
Recall that this equation finds the chance that var has not quit asof cost m by adding up all of the probabilities of 'var' quitting at costsgreater m. |
So, after substituting eq. 13 into the net benefit equation (#3b), thebenefit to 'var' is:
Notes about the equation: Notice that (V-m) is placed outsideof the integration sign. That is because in the case of 'var' against agiven fix(x=m), 'var' can never expect to win anything except V-m. So, (V-m)is a constant for a contest that can last up to any given cost m. And 'var'only wins when it has not quit as of m. And, of course, the purpose of theintegration is simply to find the chance that var will still be playingas of cost x=m. Solving eq. 14a: |
Net Benefits in Fix(x)vs. Fix(x) Contests: In this contest we have two identical fix(x)strategists facing each other. Thus, they play to exactly the same costx=m. Since we assume no other asymmetries, then it is bestto assume that two identical individuals will each win 50% of the time-- they will in effect split the net benefits. Thus:
| eq. 15: B for fix(x) vs.fix(x) =0.5 * (V - m)=0.5 * (V - x) |
Part Two: Calculation of the Costof Losing
Calculation of Cost to Var Strategists in Lossesto Fix(x): The calculations for lifetime loss costs to 'var' are a bitmore complicated than those for net benefit. The reason is that 'var'can lose to a given fix(x=m) many ways!
Here's an example.
Let's express this idea mathematically:
Let's be sure we understand what eq. 16a means:
|
We can solve eq. 16a by inserting eq. 6 for p(x) and integrating:
(presshere to see the integration) If you understand calculus and/or if you are sure that you understandhow costs are calculated, you can move on to the next section. If not, pleasevisit the following link which will take you to a discrete calculation of net benefits and costs. |
Calculation of Cost to Fix(x) Strategists When vs. Fix(x): Onceagain, this is a very easy calculation. The contestants are identical --both are willing to pay cost x=m. As we said in our considerationof benefits, we simply assume that each individual wins 0.5 (50%) times.So, half the time they lost and pay cost x=m:
eq. #17: Cost paid by a fix(x) in losingto a fix(x): = 0.5 * x = 0.5 * m |
Section A: E(fix(x=m), fix(x=m)):Let's start with fix(x) contests that end in ties (since they're easy).Now, since
eq. #2: Payoff(to Strat., when vs. a Strat.) = (Benefit from win) - (Cost from loss) if we simply substitute equations for benefit in winning (eq. 15) andcost in losing (eq. 17) we obtain: |
Section B: E(var, fix(x=m)): Thistime we substitute eqs. 14 and 16 into eq. #2 :
and if we integrate this equation we obtain the following result: (You have seen the steps to this integration previously |
At this point you can either continue on to the final proof that'var' is an ESS or you might find this a good place to take a side tripthat explores the differences between the 'var' and fix(x) strategies bypresenting graphs of benefits, costs and payoffs for each strategy. Presshere to go to a graphical presentation of |
Recall from above that to prove that 'var' is evolutionarily stable thatwe need to show that rule 2b is correct. Here we go:
Finding an Equation for the Difference in Payoffs Starting with rule 2b: E(var, fix(x)) > E(fix(x), fix(x)) and rearranging, we get: E(var, fix(x)) - E(fix(x), fix(x)) > 0 Now since: E(fix(x) ,fix(x)) = 0.5 V - m (review) and since E(var, fix(x)) = 2 * V* exp(-x/V) - V (eq. 19b) then: 2 * V* exp(-x/V) - V - 0.5*V - m > 0 which simplifies to: |
Now the big question -- is eq. 20 always positive as it must beif 'var' is an ESS?
We could start out by simply graphing it. If we do so for V=1we will see that there is no place where E(var,fix(x)) < = E(fix(x),fix(x)):
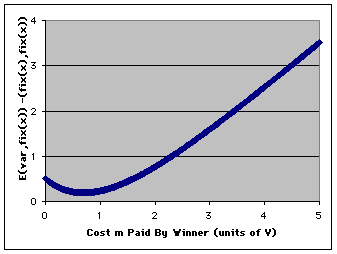
(Looks like the "swoosh" doesn't it!).
Thus, it would appear that 'var' is stable. But not so fast -- this isfor only one value of V. Is it possible that there are values of V where'var' is not evolutionarily stable? After all, V does affect 'var's behavior.
As with finding the frequency of each maximum acceptable cost (when welooked for p(x)), solving for every possible V might appear to be a difficultproblem (and approached that way, it is!). However, once again a bit ofelementary calculus can come to our aid and comfort.
Mathematical Proof: To show that no pointon eq. 20 is less than or equal to zero, we need to find the minimumvalue of eq. 20. This occurs where the slope of the graph is zero(the flat part of the graph above; on that graph it happens at a value somewherenear cost = 0.7).
Thus, 'var' is an ESS!
Graphical Illustration of the Proof: Ifyou are not fully confident that you understand the proof, you will probablybe reassured if you look at the graphs below of eq. 20 for different valuesof V. Remember, we have said that the minimum difference in fitness willalways = 0.193*V and will always occur at cost = 0.693*V:
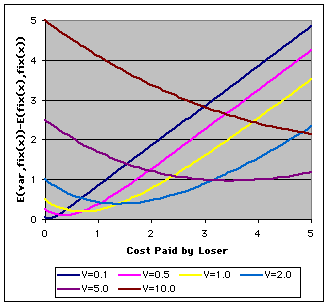
Notice that as V gets larger the minimum difference between the two payoffsincreases. (If you are "Thomas from Missouri" and want me to showyou the low V graphs inmore detail, press here.)
So there you have it. For any cost paid by the winner, m, E(var,fix(x))> E(fix(x), fix(x)). So since this is true and sinceE(var, var) = E(fix(x), var), then var is evolutionarilystable against any fix(x)!
1. Write an expression for the lifetime cost to a var strategistof quitting at a cost of exactly x. Answer 2. Write an expression for the lifetime cost to a var strategist forlosing contests where the winner was willing to pay m? Answer 3. What is E(var, fix(0)) in the caseof a tie? Answer |
Things to Remember Aboutthe 'Var' Strategy
Perhaps the most striking thing about the var strategy is thatits opponent never can know when it will quit. We have seen that the overallpattern of quitting is described by an exponential decay type of Poissondistribution with a rate constant equal to 1/V.Thus, an opponent can "learn" in generalterms what its var opponent would do. It could "know" thatit was most likely to quit early in a contest and that the chance of quittingper unit of contest display cost is exp(-1/V). From this, it is possibleto calculate (or learn from experience) the expected outcome of contestsof various costs.
However, even if it knew these things, it could never know whether ornot 'var' really would quit with the next increment of cost. Thus, no amountof experience with 'var' strategists will allow an opponent any edge overit.
The other thing to reiterate about var is that there is a logicto its quitting. It is tied to the resource value -- the greater that value,the less likely that var will quit at any particular cost and asa consequence it is potentially willing to accept a higher cost contest.Also, since 'var' always quits most frequently early in contests, the chancethat it will pay large costs relative to a resource value are low.
In the classic Clint Eastwood thriller, Dirty Harry, the Eastwoodcharacter asks a naer-do-well to predict the future and guess whether ornot there bullets left in Eastwood's gun. So what do you think? Are youfeeling lucky 1. The chance of getting killed in a scheduled commercial airline crashis roughly on the order of one in several million. It is about the samechance the earth has of being hit by a large meteor, small asteroid, orcomet. Discuss whether or not someone who flies commercial airlines daily(e.g., a flight attendant or pilot) for years is more likely on her or hisnext flight to be in a fatal accident. Likewise, the earth has notbeen hit by a really big one for about 65 million years. Are we more likelyto be hit now than we were say 60 million years ago (5 million after thelast one). Are you more likely to win on your next lottery entry (tax onstupidity) if you haven't won in the past and less likely if you have won?What does all of this have to do with the war of attrition? Discussion |
There are a number of famous examples of animals that appear to be playingsimple waiting games. We will not go into them here because they are wellpresented both in the literature and in just about every animal behaviortext book. Perhaps the classic is the dung fly, Scatophaga stercoraria,studied heavy by Parker and Parker and Thompson (refs). The interested reader is urged to consult thesepapers or any number of behavioral ecology texts. We will finish this page,however, with the following question (which was addressed by Parker andThompson):
? Suppose that someone demonstrated that animal waitingtimes corresponded to those predicted by eq. 9 Does that constitute sufficient proof that a mixedESS described by eq. #9 exists? Explain. |
Problems dealing with the calculationof P(m)
1. What is the cumulative chance of quitting between a cost of 0 andinfinity if V=1? V=5? V=0.5?
It makes no difference what the value of V is in this case. Any numberto the infinite power is infinite and the inverse of infinity is essentiallyzero. Therefore P(m) = 1.0 in all cases:
P(m)=1 - (1 / e^(infinity))=1 - (1 / infinity) = 1 - 0 = 1
2. What is the cumulative chance of quitting between a cost of 0 and0.6 if V=1? V=0.5?
For V=1: P(m = 0.6) = 1 - (1 / e^(0.6/0.5)) = 1 - (1 / e^(1.2) =
1 - (0.30) = 0.7
(return to previous placein text)
Questions About Chances ofContinuing
1. Name the probability distributions that we saw earlier that give(i) chances of continuing up to a certain cost or (ii) quitting as of acertain cost.
Ans: Q(m)and P(m),respectively
(return to previous place intext)
2. If eq. 11 gives the chance of continuing for a unit ofcost, write an expression that gives the chance of quitting per unit cost.
Ans: = 1 - exp(-1/V) -- recall that
So, for example, if V = 1, chance of quittingper unit cost is 0.632.
(return to previous place intext)
Questions About the Mixed Strategy Var
1. Compare what a contestant sees when it confrontsa population consisting entirely of 'var' strategists as compared to a populationthat is an equilibrial mix of pure supporting fix(x) strategies. Would thecontestant see any difference in these two situations?
Answer: No, they are equivalent. In both cases, the contestanthas no idea which maximum cost it is facing (provided that encounters withdifferent fix(x) supporting strategies are random in the mixed populationand that in neither case the maximum cost is tipped before being reached).
2. How would you express the idea of constantrate of quitting with respect to a population of pure strategists who togetherproduce an equilibrium?
Answer: One way would be to say that in any contest with membersof this population, there is a constant chance per increment of cost thatone' s opponent will quit. This corresponds to the idea that one's chanceof opposing a given type of supporting strategist (maximum x) would be equalto its frequency in the population (as determined by integrating eq. #6). Supportingstrategies with low maximum x values would be more common so you would bemore likely to face them.
3. Why is it crucial that no informationas to var's intention to continue or quit a contest be passed onto its opponent?
If the opponent has some reason to know var's intentions, therewill be strong selective pressure for it to act in a way that thwarts varand serves its own best interests. For instance, if it is certain that varwill not quit before reaching the opponents max cost, it will pay theopponent to quit immediately and cut its losses. Likewise, if varis certain to quit on the next move or over the next bit of cost, it willpay the opponent to wait var out and gain the resource (as comparedto var who in this case gains nothing).
(return to previous placein text)
4. How do you estimate the probabilitythat a var strategist will win a contest of cost x?
This is equal to Q(m) since Q(m) gives the chance thatvar has not quit as of cost x=m.
(return to previous placein text)
5. How do you estimate the probabilitythat a var strategist will lose a contest of cost x?
This is equal to P(m) since P(m) gives the cumulative chancethat var has already quit as of some cost x=m.
(return to previous placein text)
6. How do you estimate the probabilitythat a var strategist loses by paying a cost between x and x+dx?
This is equal to delta P(m) since delta P(m) gives thechance that var has endured to cost x=m without quitting butwill quit before paying cost x+dx (i.e., m+dm) wheredx or dm is some additional cost.
(return to previous placein text)
Calculation of the Chance of Var Paying a Specific Cost
7. Should the chance of a var quittingbetween 0.60 and 0.61 be greater or less than the chance of quitting between0.60 and 0.62? Explain.
It should be less for the smaller range of costs -- i.e., less in 0.60to 0.61 than in 0.60 to 0.62. In this case, all we have done is make a costinterval larger by 0.01. So, there are more quitting times in this largerinterval and therefore a greater total probability that an individual varwill quit within this interval.
(return to previous placein text)
8a. What is the chance of quitting withinthe specific cost interval of 0.60 and 0.61 if V=1? V=0.5?
for V=1: deltaP(m)=exp(-0.60 ) - exp(-0.61) = 0.00546
for V=0.5: deltaP(m)=exp(-0.60 / 0.5) - exp(-0.61 / 0.5) = 0.00596
(return to previous placein text)
8b. What is the cumulative chance of quittingwithin the specific cost interval of 1.0 and 1.01 if V=1? V=0.5? Comparethese answers with those you go in the last problem -- why is there a differencein probability even though delta m is the same (0.01) in both cases?
for V=1: deltaP(m)=exp(-1.0) - exp(-1.01) = 0.00366
for V=0.5: deltaP(m)=exp(-1.0 / 0.5) - exp(-1.01 / 0.5) = 0.00268
Notice that the chance of QUITTING WITHIN A SPECIFIC COST INTERVAL(delta P(m)) OF A CONSTANT RANGE (0.01) DECREASES AS THE AVERAGECOST OF THE INTERVAL INCREASES. This is not because the chance of quittingper 0.01 increment in cost has changed. Indeed, it is always proportionalto 1/V, regardless of the interval.
So why the difference? The difference reflects the lower chance thatan individual will actually have played to the higher cost. Thus, the chanceof actually having played to x = 0.60 is P(0.6) = 0.549 but the chance ofplaying all the way to x = 1.00 is P(1.00) = 0.368. If you apply a constantchance of remaining over the next 0.01x to each of these numbers (if V =1.0, it is 0.99) you will see that fewer actually quit in the second interval(because there are fewer there to quit!). There will be more about thisin the text.
(return to previous placein text)
Problems dealing with the calculationof costs to var in losses
1. Write an expression for the lifetime cost to a var strategistof quitting at a cost of exactly x.
Answer: This is given by p(x)dx and it is a very smallnumber.
Return to previous place intext
2. Write an expression for the lifetime cost to a var strategist forlosing contests where the winner was willing to pay m?
Var loses any contest that costs less than m. There are lots of waysthis can happen -- each losing cost has a unique probability of occurrencebased on 'var's probability density function. Thus:

Return to previous place intext
3. What is E(var, fix(0)) in the case ofa tie?
Following our usual rule, each side wins 50% of the time. Since thereis a 100% chance that var will play at time 0 and the cost = 0, then E(var,fix(o))=0.5*{(V-m)-m}=0.5 * (V - 0) - 0 = 0.5V.
(return to previous placein text)
Note about the term "Learn":I use the term learn loosely -- it could mean "learn" in the usualsense of learning and memory or it may be that we are simply talking aboutmaking an appropriate evolutionary response -- selection for responses thatwork against a fixed wait time. In either case, an appropriate responsearises to a particular fixed strategy.
(return to previous place in text)
"Are You Feeling Lucky, Punk?"
In the classic Clint Eastwood thriller, Dirty Harry, the Eastwoodcharacter asks a naer-do-well to predict the future and guess whether ornot there bullets left in Eastwood's gun. So what do you think? Are youfeeling lucky?
1. The chance of getting killed in a scheduled commercial airlinecrash is roughly on the order of one in several million. About the samechance the earth has of being hit by a large meteor, small asteroid, orcomet. Discuss whether or not someone who flies commercial airlines daily(e.g., a flight attendant or pilot) for years is more likely on her or hisnext flight to be in a fatal accident. Likewise, the earth has notbeen hit by a really big one for about 65 million years. Are we more likelyto be hit now than we were say 60 million years ago (5 million after thelast one). Are you more likely to win on your next lottery entry (tax onstupidity) if you haven't won in the past and less likely if you have won?What does all of this have to do with the war of attrition?
All of these chances are independent. In these cases, there is a moreor less constant probability per flight of a disaster (this might be theworst example of the three since clearly a poor pilot, bad weather, poormaintenance or whatever could change your odds) -- what happens on otherflights does not affect the next one you get on. The same with asteroidsand lottery tickets. As with 'var', a constant probability means that itcan happen any time or maybe even not at all. The main difference betweenthese examples and the war of attrition is that in the 'war' we are concernedwith the distribution of quitting costs while in the other examples theemphasis is on the constant probability of some event.
Return to your previous placein the text
Copyright © 1999 by Kenneth N. Prestwich About Fair Use of these materials Last modified 12 - 1 - 09 |